FX Forwards and Swaps
Read Post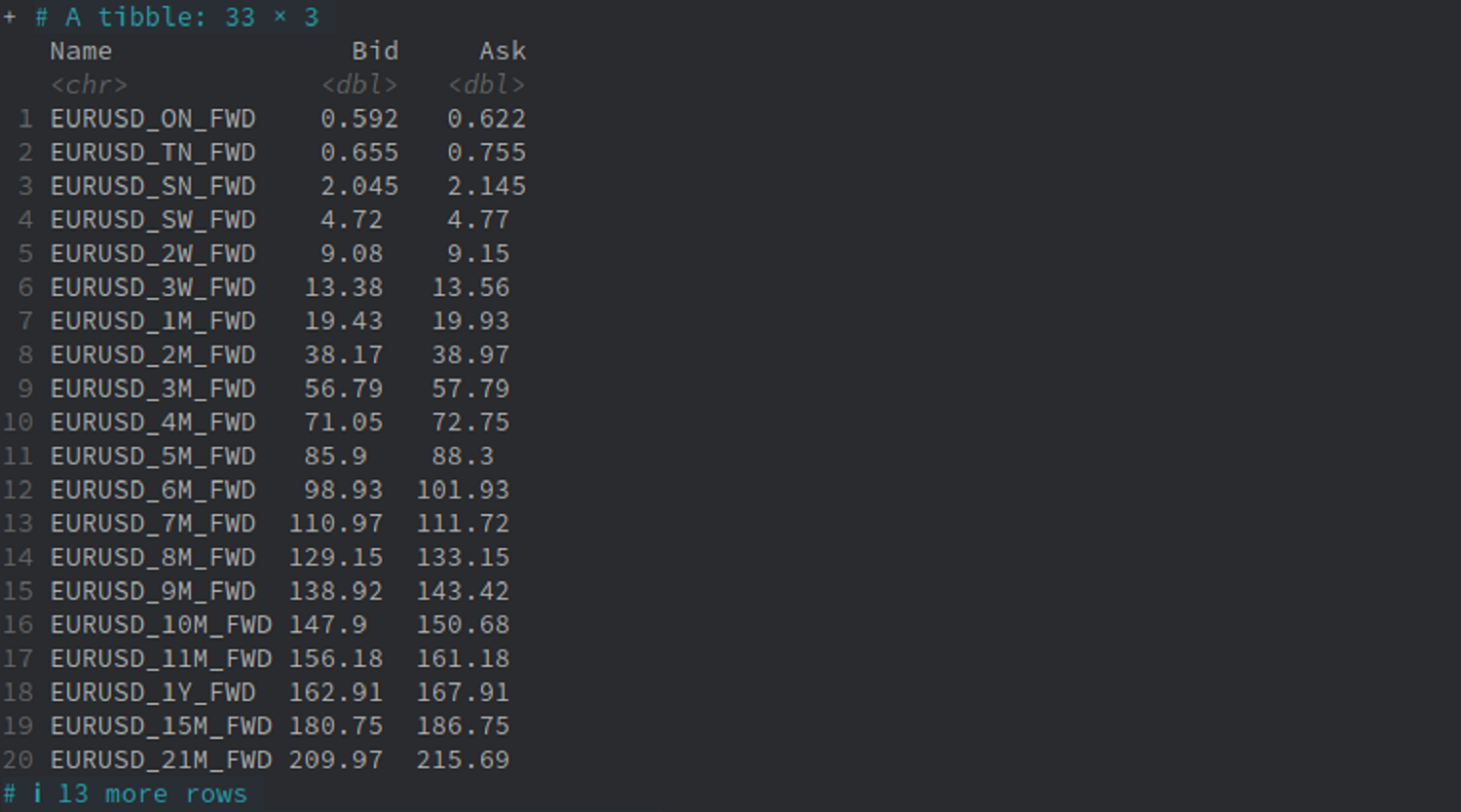
Forwards are FX contracts to fix the exchange rate in the future. As the contract involve the future, interest rates are involved. Furthermore we have to deal with two relative interest rates (interet rates differential) for the two currencies.
A FX swap involves both buying and selling a currency pair at the same time. It is a combination of a spot and forward trade.
Contents:
Forward Rate
Say you want to exchange 1 mio USD to GBP in a year’s time. You can exchange at the current spot rate and invest the GBP funds in a time deposit, or keep the USD funds in a time deposit as well and exchange to GBP at a forward rate that is determined today. The time deposit rates are known derived from Eurocurrency rates.
The forward rate would have to compensate the currency with the lower interest rate by exchanging more of the other higher currency in the future. If this is not the case, everyone would exchange spot the higher yielding currency and exchange back in the forward market, thereby eliminating the FX risk. This is also known as the arbitrage as it is a risk-free trade.
The general equation to calculate FX forward rate:
\[\begin{aligned} \text{Forward Rate} = \text{Spot} \times \frac{(1 + r_{\text{term}}\frac{T}{360})}{1 + r_{base}\frac{T}{360}} \end{aligned}\]For example, given below:
\[\begin{aligned} \text{Spot} &= 1.25\\ \text{3M EUR} &= 2\%\\ \text{3M USD} &= 1\% \end{aligned}\]Given the spot rate, 1 EUR is equivalent to 1.25 USD. Given the contract term of 91 days, the 1.25 USD will grow to a future value of:
\[\begin{aligned} 1.25 \times (1 + 0.01 \times \frac{91}{360}) \end{aligned}\]And 1 EUR will grow to a future value of:
\[\begin{aligned} 1\times(1 + 0.02 \times \frac{91}{360}) \end{aligned}\]Dividing the two will give the same answer as the forward rate formula from above.
Forward Points
It is easier to deal with forward points than forward rate as spot rate is volatile and changes alot while forward points are more stable. Forward rate can be derived from forward points by:
\[\begin{aligned} \text{Forward Rate} = \text{Spot} + \text{Forward Points} \end{aligned}\]And formula for Forward Points:
\[\begin{aligned} \text{Forward Points} &= \text{Spot} \times \Big(\frac{1 + r_{\text{term}}\frac{T}{360}}{1 + r_{\text{base}}\frac{T}{360}} - 1\Big) 100 \end{aligned}\]An approximation is:
\[\begin{aligned} \text{Forward Points} &= \text{Spot} \times (r_{term} - r_{base}) \frac{T}{360} 100 \end{aligned}\]Note that the day count convention differs for some currencies.
A simple way to know whether you are paying or earning the forward points depend on the interet rate differential. If you lose out on the interest rate (you are holding the lower yielding currency before the forward date), then you would earn the points. Likewise, if you are holding the higher yield currency, you would pay the points.
For example, we have the following info:
\[\begin{aligned} \text{USD Rates} &= 5\% \\ \text{CAD Rates} &= 7\% \\ \text{USDCAD Spot} &= 1.45 \end{aligned}\]And we want to sell CAD and buy USD forward one year into the future. The forward points are:
\[\begin{aligned} \text{Forward Points} &= 1.45 \times (7 - 5) \times \frac{365}{360} \times 100\\ &= 294 \text{ points} \end{aligned}\]In the above example, we will be assumed to be holding CAD for a year. As CAD is the higher yielding currency, we will be paying the points. In other words, we will be able to sell the CAD forward in the future at a higher rate than the current spot rate. In other words, pay more CAD and get less USD.
\[\begin{aligned} \text{USDCAD 1Y Forward} &= 1.45 + \frac{294}{10000}\\ &= 1.4794 \end{aligned}\]Let us do another example with negative points:
\[\begin{aligned} \text{USD Rates} &= 5\% \\ \text{EUR Rates} &= 4\% \\ \text{EURUSD Spot} &= 1.52 \end{aligned}\]And we want to buy EUR and sell USD forward one year into the future. The forward points are:
\[\begin{aligned} \text{Forward Points} &= 1.52\times (4 - 5) \times \frac{365}{360} \times 100\\ &= -154 \text{ points} \end{aligned}\]In this example, we are holding USD and it is the higher yielding currency. So again in this case we are paying the points for earning the interest rate differential, by getting less EUR per USD:
\[\begin{aligned} \text{EURUSD 1Y Forward} &= 1.52 - \frac{154}{10000}\\ &= 1.5046 \end{aligned}\]Bid and Offer
We can easily tell from the Bid/Offer spread whether the points are premium or discount points. If the bid is lower than the offer, the points will be added to the spot rate:
\[\begin{aligned} \text{Bid-Offer} &= \text{215-220}\\ \text{Spot} &= 1.5690\\ \text{Bid Forward Points} &= 1.5690 + 0.0215\\ &= 1.5905\\ \text{Offer Forward Points} &= 1.5690 + 0.0220\\ &= 1.5910\\ \end{aligned}\]And if the bid is higher than the offer, the points will be subtracted from the spot rate:
\[\begin{aligned} \text{Bid-Offer} &= \text{149-148}\\ \text{Spot} &= 1.0130\\ \text{Bid Forward Points} &= 1.0130 - 0.0149\\ &= 0.9981\\ \text{Offer Forward Points} &= 1.0130 - 0.0148\\ &= 0.9982\\ \end{aligned}\]If done correctly, the offer will always be higher than the bid.
O/N and T/N
If the delivery date is before the spot date, then we would have to reverse the forward points as now the far dated is the spot value date or \((T-1)\) instead. We will cover this later in the FX swap section as this only make sense for FX swaps.
Scrap Data
Let us use R to scrap Forwards data from investing.com:
library(rvest)
url <- "https://www.investing.com/rates-bonds/forward-rates"
page <- read_html(
paste0(url)
)
page |>
html_nodes("#curr_table") |>
html_table() |>
nth(1) |>
select(Name, Bid, Ask) |>
mutate(
Name = gsub(" ", "_", Name)
) |>
print(n = 20)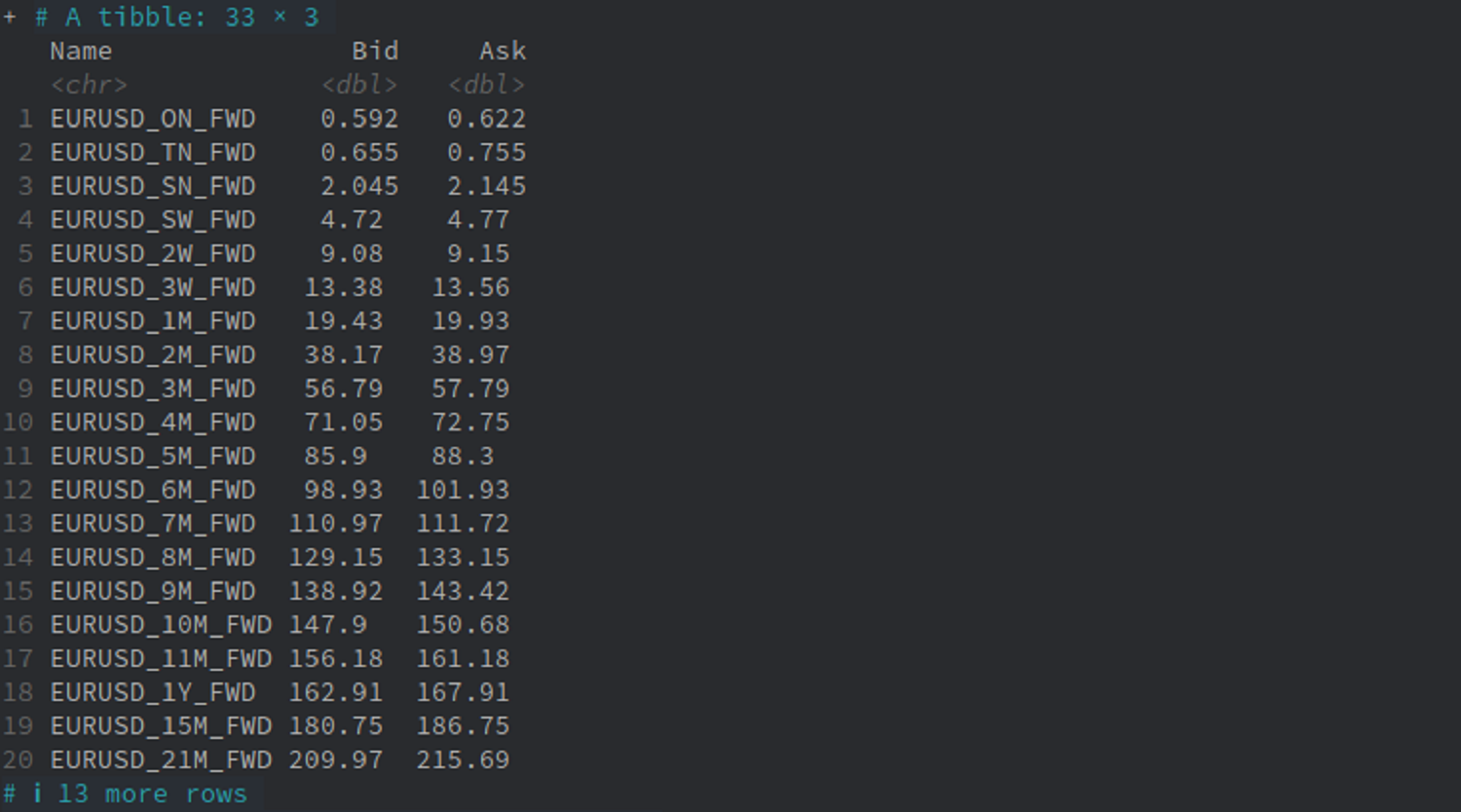
FX Swap
An FX swap is a transaction that exchanges one currency for another for a period of time. There is a buy/sell swap that buys the base currency in the near date and sell the base currency swap. Likewise for a sell/buy swap.
Short-Dated swaps are swaps with a forward date that is less than a month. Otherwise it is known as a forward swap.
Bid and Offer
When you see a market bid/offer swap quote, how do you know which one to hit? Always refer to the far-dated leg. If you are doing a buy/sell swap, hit the bid, and sell/buy hit the offer.
For example, a client wants to buy/sell a GBPUSD 1Y swap. Given the following info:
\[\begin{aligned} \text{Spot} &= 1.5975\\ \text{Forward Points}_{\text{Bid-Offer}} &= 334-301\\ \end{aligned}\]As the far dated leg is short, we would use the bid points. Note the bid is more than the offer, so we would subtract the points off the spot.
\[\begin{aligned} \text{1Y Forward Price} &= 1.5975 - \frac{334}{10000}\\ &= 1.5641 \end{aligned}\]Check the work. As we are paying the points, we are selling GBPUSD at a lower rate compared to the spot rate.
The interest rates used to derive the bid/offer forward points have its own bid/offer Eurocurrency rates as well. In the FX market, one buy and sell a currency, while in Eurocurrency market, one borrow and lends instead.
Basically, the bid side of the swap market corresponds to the offered side of the Eurocurrency market, and the offer side of the swap market corresponds to the bid side of the Eurocurrency market. This is because when market maker buy a swap forward, the market maker is short the base currency. This is equivalent to loaning the base currency, which is the offered side from a market maker. Similarly, if the marketmaker sell a swap forward, the market maker is long the base currency, and this is equivalent to borrowing the base currency in the Eurocurrency market on the bid side.
Swap Points
The swap points are exactly the same as the forward points but in this section, we will incorporate the bid/offer as well. Note that the bid/offer calculation applies to forwards as well.
\[\begin{aligned} \text{Swap Points}_{\text{Bid}} &= \text{Spot}\times(r_{\text{term bid}} - r_{\text{base offer}})\frac{T}{360}100\\ \text{Swap Points}_{\text{Offer}} &= \text{Spot}\times(r_{\text{term offer}} - r_{\text{base bid}})\frac{T}{360}100 \end{aligned}\]In the forwards section, we determine whether we pay or earn the points depending on the interest rate of the currency currently holding (assuming it is covered) is higher or lower than the other currency’s interest. If the interest is lower, you earn the points. If lower, you pay the points. The same applies to swap points as well.
A quicker way is to determine whether you add or subtract the swap points from spot rate. This applies the same whether one is long or short a swap. All one needs to know is whether the base currency rate is higher or lower than the term currency rate.
If the base rate is higher, subtract the points:
If you are selling the base currency at the forward date, you will be holding the base currency. Given the higher rate, you will sell the base currency forward at a reduced rate.
Likewise, if you are buying the base currency at the forward rate, you will be holding the lower yielding term currency. To compensate that, you will buy the base currency at a reduced rate as well.
If the base rate is lower, add the points:
If you are selling the base currency at the forward date, you will be holding the base currency. Given the lower rate, you will sell the base currency forward at a higher rate.
Likewise, if you are buying the base currency at the forward rate, you will be holding the higher yielding term currency. To compensate that, you will buy the base currency at a higher rate as well.
Interest Rate Outlook
When trading a swap, you are trading the interest rate differential between the two currencies. If you expect the differential to widen, you will pay the “loser” points first expecting the points to widen/increase in the future. Likewise, if you expect the differential to narrow, you sell the “higher” points first, expecting the points to narrow/decrease in the future.
Usage of FX Swap
Example 1
For example, a bank sold a 10mio 3M EURUSD FX forward with a client. Concurrently, it would hedge its position by doing a 10mio FX spot trade. This would require an inflow of USD which wouldn’t come in until 3M time. In the mean time, the bank could borrow the USD and lend out the 10mio EUR. But usually the bank will resolve the liquidity issue by executing a FX swap:
\[\begin{aligned} \text{Spot}_{\text{Mid}} &= 1.2502\\[5pt] \text{3M}_{\text{Bid-Offer}} &= 38-40 \end{aligned}\]Because now the market maker is a market user, it would hit the offer as it is buying EUR on the far leg.
\[\begin{aligned} \text{Forward} &= 1.2502 + \frac{40}{10000}\\ &= 1.2542 \end{aligned}\]To conclude, on the near date, the positions are squared as the EUR that is coming in from the spot trade is offset with an outflow from the near leg of the FX swap. Similarly, the outflow of USD from the spot trade is offset by the inflow of the USD from the FX swap. Finally, the positions is squared on the far date. As you can see from the premium swap points, the bank earns the points in this example.
Example 2
In the next example, given:
\[\begin{aligned} \text{Spot}_{\text{Mid}} &= 1.4500\\[5pt] \text{TN}_{\text{Bid-Offer}} &= \text{0.5-1} \end{aligned}\]Now the bank bought a 10mio EURUSD from a client. It would hedge by doing a FX spot trade and sell 10mio EURUSD. It will resolve the liquidity issue by selling EUR TN and buying EUR spot:
\[\begin{aligned} \text{Forward} &= 1.24500 - \frac{1}{10000}\\ &= 1.2449 \end{aligned}\]The bank would sell EURUSD TN at 1.2449 and buy EURUSD spot at 1.24500.
Example 3
Banks also use FX swaps to regulate their cash positions. Of example, if a bank has an overnight surplus of EUR, lend out the EUR or it can execute a ON/TN EURUSD swap to sell EUR ON and buy it back on TN. For example given:
\[\begin{aligned} \text{1M GBP} &= 3\% \\ \text{1M USD} &= 1\% \\[5pt] \text{Swap Points}_{\text{Bid-Ask}} &= \text{17-19}\\[5pt] \text{Spot} &= 1.2500\\ \text{Forward} &= 1.2519 \end{aligned}\]If the bank lends out its excess 20 mio GBP and borrows 25 mio USD for 1M:
\[\begin{aligned} \text{Interest}_{\text{GBP}} &= \text{20,000,000} \times 0.03 \times \frac{31}{365}\\ &= \text{50,958.90}\\ \text{Interest}_{\text{USD}} &= \text{25,000,000} \times 0.03 \times \frac{31}{360}\\ &= \text{107,638.89} \end{aligned}\]Note that the day count convention for GBP is \(\frac{T}{365}\). Converting USD 107,638.89 by the forward rate (buy GBP forward):
\[\begin{aligned} \text{107,638.89} \times 1.2519 &= \text{GBP 85,980.42} \end{aligned}\]The net interest rate cost:
\[\begin{aligned} \text{85,98.42} - \text{50,958.90} &= \text{GBP 35,021.52} \end{aligned}\]Alternatively, the bank can execute a sell buy 1M GBPUSD FX swap. It will sell 20 mio GBP for 25 mio USD and swap the 25 mio USD to:
\[\begin{aligned} \frac{\text{25,000,000}}{1.2519} &= \text{USD 19,969,646.13}\\[5pt] \text{Interest}_{GBP} &= \text{20,000,000} - \text{19,969,646.13} \\ &= \text{GBP 30,353.87} \end{aligned}\]As you can see, the FX swap interest cost is lower than the money market interest.
Example 4 Synthetic Loan
Sometimes it is possible to take a loan in another currency and swap it back to the home currency. Usually this would not be possible as the interest differential would be priced into the swap points but sometimes arbitrage opportunities are available.
For example, a French company wants to issue a 30 days commercial paper and a funding requirement of 8mio EUR. The company is thinking of taking a loan in USD and swap it back to EUR.
The following info is given:
\[\begin{aligned} \text{1M EUR} &= 3.6\% \\ \text{1M USD} &= 5.6\% \\ \text{Spot} &= 1.2500\\ \text{Forward Points} &= 22 \end{aligned}\]The issue discount price of a USD commerical paper:
\[\begin{aligned} \text{Price} &= \frac{\text{USD 10mio}}{1 + \frac{30}{360} \times 0.056}\\ &= \text{USD 9,953,550.10} \end{aligned}\]Swapping this at the spot rate of 1.2500:
\[\begin{aligned} \frac{\text{USD 9,953,550.10}}{1.2500} &= \text{EUR 7,962,840.08} \end{aligned}\]And eventually buying it back at the forward rate of 1.2522:
\[\begin{aligned} \frac{\text{USD 10,000,000}}{1.2522} &= \text{EUR 7,985,944.74} \end{aligned}\]The interest:
\[\begin{aligned} \frac{\text{EUR 7,985,944.74} - \text{EUR 7,962,840.08}}{\text{EUR 7,962,840.08}} &= \frac{\text{EUR 23,104.66}}{\text{EUR 7,962,840.08}}\\ &= 0.00290 \% \end{aligned}\]And annualized:
\[\begin{aligned} 0.00290 \% \times \frac{360}{3} &= 3.48 \% \end{aligned}\]Note that the interest is lower than 3.6%.
Synthetic Loan
You can use the following calculation to determine the interest rate implied by the swap points.
For Term Currency:
\[\begin{aligned} r_{\text{term}} &= \Bigg[\Big[\Big( 1 + r_{\text{base}} \times \frac{T}{360} \times \frac{\text{Forward}}{\text{Spot}}Big)\Big] - 1\Bigg] \times \frac{360}{T} \end{aligned}\]For Base Currency:
\[\begin{aligned} r_{\text{base}} &= \Bigg[\Big[\Big( 1 + r_{\text{term}} \times \frac{T}{360} \times \frac{\text{Spot}}{\text{Forward}}Big)\Big] - 1\Bigg] \times \frac{360}{T} \end{aligned}\]For example, given:
\[\begin{aligned} \text{EURGBP Spot} &= 0.900\\ \text{1M Swap Points} &= \text{9-10}\\ \text{EUR}_{1M} &= \text{1.00-1.01}\% \\ \text{GBP}_{1M} &= \text{2.17-2.18}\% \end{aligned}\]If the trader can borrow at the GBP ask rate of 2.18% for 31 days (note DCF of GBP is \(\frac{31}{365}\)):
\[\begin{aligned} r_{\text{term}} &= \Bigg[\Big[\Big( 1 + 0.0218 \times \frac{31}{365} \times \frac{\text{Forward}}{\text{Spot}}Big)\Big] - 1\Bigg] \times \frac{365}{31}\\ &= 0.99 \% \end{aligned}\]Hence there is an arbitrage opportunity here. The trader can borrow at 0.99% and invest via FX swap to earn 1%.
Trading FX Swap
To trade a view on interest rate differentials, trader can take a spread position depending on the direction of the differentials. For example, if the view is that the differentials will increase over time, the trader can take a long positions that have swap points in your favor, and a short position in swap points in their favor. Reverse if the view is the differentials will narrow.
For example, given below and the view that EURUSD swap points will narrow:
\[\begin{aligned} \text{EURUSD Spot} &= 1.3500\\ \text{3M Swap Points} &= \text{30-35}\\ \text{6M Swap Points} &= \text{62-68} \end{aligned}\]Because EUR is trading at a premium, being short EUR forward will be in your favor. So long 6M and short 3M. So sell/buy 6M and buy/sell 3M.
Cashflow at t = 0:
\[\begin{aligned} \text{3M Swap} &= \text{-1,000 EUR, +1,3500 USD}\\ \text{6M Swap} &= \text{+1,000 EUR, -1,3500 USD}\\ \end{aligned}\]At t = 0, the position will be flat as the long EUR will be offset with the short EUR.
At t = 3M, given the following narrower swap points:
\[\begin{aligned} \text{EURUSD Spot} &= 1.3500\\ \text{3M Swap Points} &= \text{20-25} \end{aligned}\]Initiate another buy/sell 3M swap at swap points of 20. Assuming the spot rate is the same as the forward rate 1.3535 (unrealistic). Cashflow at t = 3M:
\[\begin{aligned} \text{3M Swap} &= \text{+1,000 EUR, -1,3535 USD}\\ \text{3M Swap} &= \text{-1,000 EUR, +1,3535 USD}\\ \end{aligned}\]Finally at t = 6M:
\[\begin{aligned} \text{3M Swap} &= \text{-1,000 EUR, -1,3560 USD}\\ \text{6M Swap} &= \text{+1,000 EUR, +1,3562 USD}\\ \end{aligned}\]So we gain $2 in USD:
\[\begin{aligned} \text{1,3562 - 1,3560} &= 2 \end{aligned}\]Value Today/Tomorrow (Ex-Ante)
Delivery of a FX transaction is usually done T+2, but it can be done value same day (T+0) or value tomorrow (T+1). Same day delivery, if cleared by CLS bank, has to be done before TARGET2 cut-off time (6:30am CET). Certain currency pair cannot clear same day, for example JPY as BOJ closes at 7am CET.
For premium or discount forward points, the calculation has to be reversed for ex-ante dates.
For example, given these discount forward points for GBPUSD:
\[\begin{aligned} \text{Spot}_{\text{Bid-Offer}} &= \text{1.2500-1.2502}\\[5pt] \text{ON}_{\text{Bid-Offer}} &= \text{2-1.5}\\[5pt] \text{TN}_{\text{Bid-Offer}} &= \text{3-2.5} \end{aligned}\]When the bid is higher than the offer, we would deduct the points. But for ex-ante dates, in order to make the ex-ante points higher than spot, we would need to add instead and swap the bid/offer to maintain the offer higher than the bid:
\[\begin{aligned} \text{TN}_{\text{Bid}} &= 1.2500 + \frac{2.5}{10000}\\ &= 1.25025\\ \text{TN}_{\text{Offer}} &= 1.2502 + \frac{3}{10000}\\ &= 1.2505\\[5pt] \text{ON}_{\text{Bid}} &= 1.25025 + \frac{1.5}{10000}\\ &= 1.2500 + \frac{2.5}{10000} + \frac{1.5}{10000}\\ &= 1.2500 + \frac{4}{10000}\\ &= 1.2504\\ \text{ON}_{\text{Offer}} &= 1.2505 + \frac{2}{10000}\\ &= 1.2502 + \frac{3}{10000} + \frac{2}{10000}\\ &= 1.2502 + \frac{5}{10000}\\ &= 1.2507 \end{aligned}\]Given the following premium forwards points EURUSD example:
\[\begin{aligned} \text{Spot}_{\text{Bid-Offer}} &= \text{1.3500-1.3502}\\[5pt] \text{ON}_{\text{Bid-Offer}} &= \text{0.75-1.25}\\[5pt] \text{TN}_{\text{Bid-Offer}} &= \text{0.5-1} \end{aligned}\]Usually we will add the points if premium. But in this case, we would reverse the bid/offer and subtract the points:
\[\begin{aligned} \text{TN}_{\text{Bid}} &= 1.3500 - \frac{1}{10000}\\ &= 1.3499\\ \text{TN}_{\text{Offer}} &= 1.3502 - \frac{0.5}{10000}\\ &= 1.35015\\[5pt] \text{ON}_{\text{Bid}} &= 1.3499 - \frac{1.25}{10000}\\ &= 1.3500 - \frac{1}{10000} - \frac{1.25}{10000}\\ &= 1.3499 - \frac{2.25}{10000}\\ &= 1.349775\\ \text{ON}_{\text{Offer}} &= 1.35015 - \frac{0.75}{10000}\\ &= 1.3502 - \frac{0.75}{10000} + \frac{0.5}{10000}\\ &= 1.3502 - \frac{1.25}{10000}\\ &= 1.350075 \end{aligned}\]Date Conventions (Modified Following)
Forward value date is always based on number of business days. Follow the date rules below step by step:
Step1: Date-to-Date
For example, if the spot date is Jul 6th, a 1M forward expiry date would be Aug 6th.
Step2: Holidays/Weekends
If the forward date is a holiday or a weekend, move the forward value date to the next business day. For example, if Aug 6th is a holiday, move to Aug 7th.
Step3: End-to-End
If the spot date is the last business day of the month, the forward value date has to be the last business day of the month as well.
Odd Dates
If the dates do not fall nicely according to standard date conventions, one can interpolate the rates by the number of days between two standard dates.
For example, a client want to sell EUR 197 days forward:
\[\begin{aligned} \text{6 months} &= 181 \text{ days}\\ \text{7 months} &= 212 \text{ days}\\ \text{6M Forward}_{\text{Bid}} &= -83.2\\ \text{7M Forward}_{\text{Bid}} &= -95.5\\ \end{aligned}\] \[\begin{aligned} \text{197D Forward} &= (83.2 - 95.5)\frac{197 - 181}{212 - 181} \end{aligned}\]Carry Trade
An example of a positive carry trade involving USDJPY.
Given the following:
\[\begin{aligned} \text{SN Points} &= -0.45\\ \text{3Y Forward Points} &= \text{-1,040}\\ &= -0.95 \times 365\\ &= -0.95 \text{/day} \end{aligned}\]As the 3Y forward points is higher than SN (a positive carry of 0.5 points), we can sell a 3Y 1mio FX swap and fund the trade by rolling over a SN swap every day assuming the SN rate doesn’t change much. On the day when we sell the 3Y swap, we will be short USD and long JPY. The SN swap will sell the JPY and buy USD for one day.
The carry is calculated as:
\[\begin{aligned} \text{1,000,000} \times \frac{0.95 - 0.45}{100}\frac{1}{120} &= 417 \text{/day} \end{aligned}\]As we are short USD on the long end, we are hoping the USD rates to go down so that we can roll over at a lower rate each day.
