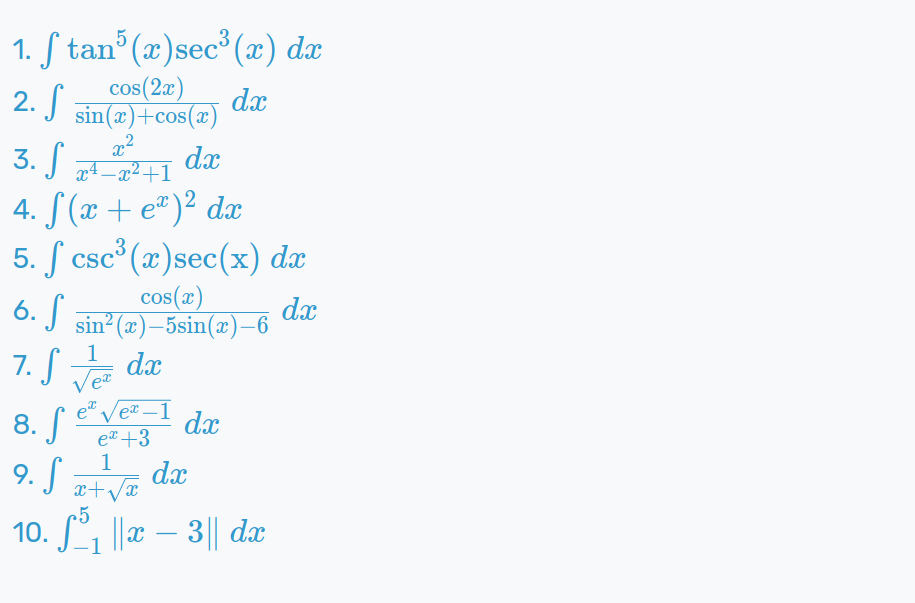
This post document the solutions to 100 integrals (Problem 1 to 10) solved by @blackpenredpen in his 5h++ marathon endeavor.

1. \(\int \mathrm{tan}^{5}(x)\mathrm{sec}^{3}(x)\ dx\)

\[\begin{aligned} \int \mathrm{tan}^{5}(x)\mathrm{sec}^{3}(x)\ dx &= \int \mathrm{tan}^{4}(x)\mathrm{sec}^{2}(x)\ \mathrm{tan}(x)\mathrm{sec}(x)\ dx \end{aligned}\]

Trig Substitution:

\[\begin{aligned} u &= \mathrm{sec}(x)\\ du &= \mathrm{sec}(x)\mathrm{tan}(x)\ dx \end{aligned}\] \[\begin{aligned} \int (u^{2} - 1)^{2}u^{2}\ du &= \int u^{6} - 2u^{4} + u^{2}\ du\\ &= \frac{1}{7}u^{7} - \frac{2}{5}u^{5} + \frac{1}{3}u^{3} + C\\ &= \frac{1}{7}\mathrm{sec}^{7}(x) - \frac{2}{5}\mathrm{sec}^{5}(x) + \frac{1}{3}\mathrm{sec}^{3}(x) + C \end{aligned}\]

2. \(\int \frac{\mathrm{cos}(2x)}{\mathrm{sin}(x) + \mathrm{cos}(x)}\ dx\)

Double-Angle Formula:

\[\begin{aligned} \mathrm{cos}(2x) &= \mathrm{cos}^{2}(x) - \mathrm{sin}^{2}(x) \end{aligned}\] \[\begin{aligned} \int \frac{\mathrm{cos}(2x)}{\mathrm{sin}(x) + \mathrm{cos}(x)}\ dx &= \int \frac{\mathrm{cos}^{2}(x) - \mathrm{sin}^{2}(x)}{\mathrm{sin}(x) + \mathrm{cos}(x)} \ dx\\ &= \int \frac{\Big(\mathrm{cos}(x) - \mathrm{sin}(x)\Big)\Big(\mathrm{cos}(x) + \mathrm{sin}(x)\Big)}{\mathrm{sin}(x) + \mathrm{cos}(x)}\ dx\\ &= \int \mathrm{cos}(x) - \mathrm{sin}(x) \ dx\\ &= \mathrm{sin}(x) + \mathrm{cos}(x) + C \end{aligned}\]

3. \(\int \frac{x^{2}}{x^{4} - x^{2} + 1} \ dx\)

\[\begin{aligned} \int \frac{x^{2}}{x^{4} - x^{2} + 1} \ dx &= \int \frac{1 + \frac{1}{x^{2}}}{x^{2} - 1 + \frac{1}{x^{2}}}\ dx\\ &= \int \frac{1 + \frac{1}{x^{2}}}{x^{2} - 2 + \frac{1}{x^{2}} + 1}\ dx\\ &= \int \frac{1 + \frac{1}{x^{2}}}{\Big(x - \frac{1}{x}\Big)^{2} + 1}\ dx \end{aligned}\]

Trig Substitution:

\[\begin{aligned} u & = x - \frac{1}{x}\\ du &= \Big(1 + \frac{1}{x^{2}}\Big)\ dx \end{aligned}\] \[\begin{aligned} \int \frac{1}{u^{2} + 1}\ du &= \mathrm{tan}^{-1}(u) + C\\ &= \mathrm{tan}^{-1}\Big(x - \frac{1}{x}\Big) + C \end{aligned}\]

4. \(\int (x + e^{x})^{2} \ dx\)

\[\begin{aligned} \int (x + e^{x})^{2} \ dx &= \int x^{2} + 2xe^{x} + e^{2x}\ dx \end{aligned}\]

Integration by parts:

\[\begin{aligned} u &= 2x\\ dv &= e^{x} \ dx\\ v &= e^{x}\\ du &= 2 dx\\ \int u \ dv &= uv - \int v\ du\\ &= 2xe^{x} - \int 2e^{x}\ dx\\ &= 2xe^{x} - 2e^{x}\ dx \end{aligned}\] \[\begin{aligned} \int x^{2} + 2xe^{x} + e^{2x}\ dx &= \frac{1}{3}x^{3} + 2xe^{x} - 2e^{x} + \frac{1}{2}e^{2x} + C \end{aligned}\]

5. \(\int \mathrm{csc}^{3}(x)\mathrm{sec}(x)\ dx\)

Pythagorean Identity:

\[\begin{aligned} \mathrm{sin}^{2}(x) + \mathrm{cos}^{2}(x) = 1 \end{aligned}\] \[\begin{aligned} \int \mathrm{csc}^{3}(x)\mathrm{sec}(x)\ dx &= \int \frac{1}{\mathrm{sin}^{3}(x)\mathrm{cos}(x)}\ dx\\[3pt] &= \int \frac{\mathrm{sin}^{2}(x) + \mathrm{cos}^{2}(x)}{\mathrm{sin}^{3}(x)\mathrm{cos}(x)}\ dx\\[3pt] &= \int \frac{\mathrm{sin}^{2}(x)}{\mathrm{sin}^{3}(x)\mathrm{cos}(x)} + \frac{\mathrm{cos}^{2}(x)}{\mathrm{sin}^{3}(x)\mathrm{cos}(x)}\ dx\\[3pt] &= \int \frac{1}{\mathrm{sin}(x)\mathrm{cos}(x)} + \frac{\mathrm{cos}(x)}{\mathrm{sin}^{3}(x)}\ dx\\[3pt] &= \int \frac{\mathrm{sin}^{2}(x) + \mathrm{cos}^{2}(x)}{\mathrm{sin}(x)\mathrm{cos}(x)} + \frac{\mathrm{cos}(x)}{\mathrm{sin}^{3}(x)}\ dx\\[3pt] &= \int \frac{\mathrm{sin}^{2}(x)}{\mathrm{sin}(x)\mathrm{cos}(x)} + \frac{\mathrm{cos}^{2}(x)}{\mathrm{sin}(x)\mathrm{cos}(x)} + \frac{\mathrm{cos}(x)}{\mathrm{sin}^{3}(x)}\ dx\\[3pt] &= \int \frac{\mathrm{sin}(x)}{\mathrm{cos}(x)} + \frac{\mathrm{cos}(x)}{\mathrm{sin}(x)} + \frac{\mathrm{cos}(x)}{\mathrm{sin}^{3}(x)}\ dx\\[3pt] &= \int \mathrm{tan}(x) + \mathrm{cot}(x) + \frac{\mathrm{cos}(x)}{\mathrm{sin}^{3}(x)}\ dx\\[3pt] &= \mathrm{ln}|\mathrm{sec}(x)| + \mathrm{ln}|\mathrm{sin}(x)| + \int \frac{\mathrm{cos}(x)}{\mathrm{sin}^{3}(x)}\ dx \end{aligned}\]

Trig Substitution:

\[\begin{aligned} u & = \mathrm{sin}(x)\\ du &= \mathrm{cos}(x)\ dx\\ \int \frac{1}{u^{3}}\ du &= \frac{1}{2 u^{2}}\\ &= \frac{1}{2 \mathrm{sin}^{2}(x)} \end{aligned}\] \[\begin{aligned} \mathrm{ln}|\mathrm{sec}(x)| + \mathrm{ln}|\mathrm{sin}(x)| + \int \frac{\mathrm{cos}(x)}{\mathrm{sin}^{3}(x)}\ dx &= \mathrm{ln}|\mathrm{sec}(x)| + \mathrm{ln}|\mathrm{sin}(x)| - \frac{1}{2 \mathrm{sin}^{2}(x)} + C\\ &= \mathrm{ln}|\mathrm{sec}(x)\mathrm{sin}(x)| - \frac{1}{2 \mathrm{sin}^{2}(x)} + C\\ &= \mathrm{ln}|\mathrm{tan}(x)| - \frac{1}{2}\mathrm{csc}^{x} + C \end{aligned}\]

6. \(\int \frac{\mathrm{cos}(x)}{\mathrm{sin}^{2}(x) - 5\mathrm{sin}(x) - 6}\ dx\)

\[\begin{aligned} \int \frac{\mathrm{cos}(x)}{\mathrm{sin}^{2}(x) - 5\mathrm{sin}(x) - 6}\ dx \end{aligned}\]

Trig Substitution:

\[\begin{aligned} u &= \mathrm{sin}(x)\\ du &= \mathrm{cos}(x)\ dx \end{aligned}\] \[\begin{aligned} \int \frac{1}{u^{2} - 5u - 6}\ du &= \int \frac{1}{(u - 6)(u +1)} \ du\\[5pt] &= \int \frac{\frac{1}{7}}{u - 6} - \frac{\frac{1}{7}}{u + 1} \ du\\[5pt] &= \frac{1}{7}\mathrm{ln}\Big|\frac{u - 6}{u + 1}\Big| + C\\[5pt] &= \frac{1}{7}\mathrm{ln}\Big|\frac{\mathrm{sin}(x) - 6}{\mathrm{sin}(x) + 1}\Big| + C \end{aligned}\]

7. \(\int \frac{1}{\sqrt{e^{x}}}\ dx\)

\[\begin{aligned} \int \frac{1}{\sqrt{e^{x}}}\ dx &= \int \frac{1}{e^{\frac{x}{2}}}\ dx\\ &= \int e^{-\frac{x}{2}}\ dx\\ &= -2e^{-\frac{x}{2}} + C\\ &= \frac{-2}{\sqrt{e^{x}}} + C \end{aligned}\]

8. \(\int \frac{e^{x}\sqrt{e^{x} - 1}}{e^{x} + 3}\ dx\)

\[\begin{aligned} \int \frac{e^{x}\sqrt{e^{x} - 1}}{e^{x} + 3}\ dx \end{aligned}\]

Trig Substitution:

\[\begin{aligned} u &= \sqrt{e^{x} - 1}\\ du &= \frac{e^{x}}{2\sqrt{e^{x} - 1}}\ dx\\[5pt] dx &= \frac{2\sqrt{e^{x} - 1}}{e^{x}} \ du\\[5pt] dx &= \frac{2u}{e^{x}} \ du\\[5pt] u^{2} &= e^{x} - 1\\[5pt] u^{2} + 1 &= e^{x}\\[5pt] \end{aligned}\] \[\begin{aligned} \int \frac{e^{x}\sqrt{e^{x} - 1}}{e^{x} + 3}\ dx &= \int \frac{e^{x}u}{(u^{2} + 1) + 3} \frac{2u}{e^{x}} \ du\\[5pt] &= 2\int \frac{u^{2}}{u^{2} + 4} \ du\\[5pt] &= 2\int \frac{u^{2} - 4 + 4}{u^{2} + 4} \ du\\[5pt] &= 2\int \frac{u^{2} - 4}{u^{2} + 4} + \frac{4}{u^{2} + 4} \ du\\[5pt] &= 2\Big(\int 1 \ du - 4\int \frac{1}{u^{2} + 2^{2}}\ du\Big)\\[5pt] &= 2 \Big(u - 4\times\frac{1}{2}\mathrm{tan}^{-1}\Big(\frac{u}{2}\Big)\Big) + C\\[5pt] &= 2 \sqrt{e^{x} - 1} - 4\mathrm{tan}^{-1}(\frac{\sqrt{e^{x} - 1}}{2}) + C \end{aligned}\]

9. \(\int \frac{1}{x + \sqrt{x}}\ dx\)

\[\begin{aligned} \int \frac{1}{x + \sqrt{x}}\ dx &= \int \frac{1}{\sqrt{x}(\sqrt{x} + 1)}\ dx \end{aligned}\]

Trig Substitution:

\[\begin{aligned} u &= \sqrt{x} + 1\\ du &= \frac{1}{2\sqrt{x}}\ dx\\ dx &= 2\sqrt{x}\ du \end{aligned}\] \[\begin{aligned} \int \frac{1}{\sqrt{x}(\sqrt{x} + 1)}\ dx &= \int \frac{1}{\sqrt{x}u}2\sqrt{x}\ du\\ &= \int \frac{2}{u}\ du\\ &= 2 \mathrm{ln}|\sqrt{x} + 1| + C\\ &= 2 \mathrm{ln}(\sqrt{x} + 1) + C \end{aligned}\]

10. \(\int_{-1}^{5} |x - 3| \ dx\)

Draw a graph of \(\|x - 3\|\) and add up the 2 triangles:

\[\begin{aligned} \int_{-1}^{5} |x - 3| \ dx &= \frac{1}{2}\times 4^{2} + \frac{1}{2}\times 2^{2}\\ &= 8 + 2\\ &= 10 \end{aligned}\]

See Also

Problem 11 to 20

Problem 21 to 30

References

100 integrals (world record?) @blackpenredpen