Time Series Analysis - Classical Regression
Read PostIn this post, we will cover Shumway H. (2017) Time Series Analysis, focusing on classical regression.
Contents:
Datasets
Let us look at the datasets we will be using in this post. All the datasets can be found in the astsa package.
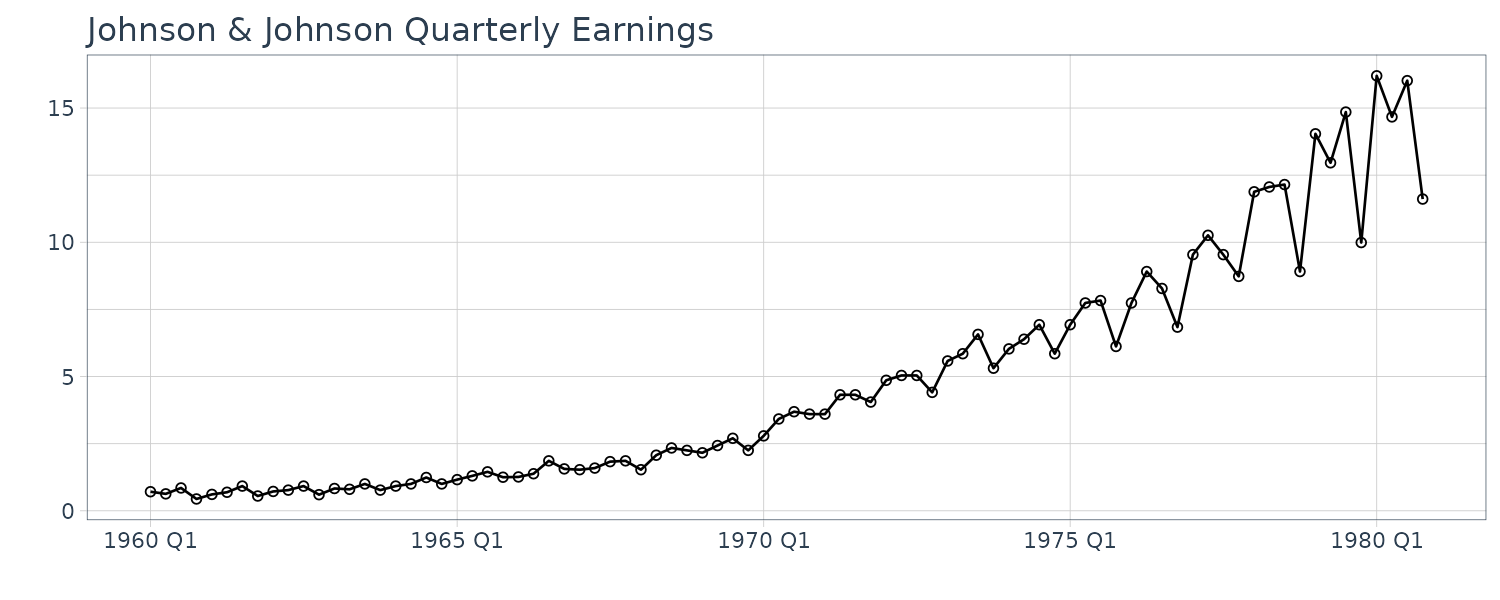
Johnson & Johnson Quarterly Earnings
Quarterly earnings per share of Johnson $ Johnson from 1960 to 1980 for a total of 84 quarters (21 years).
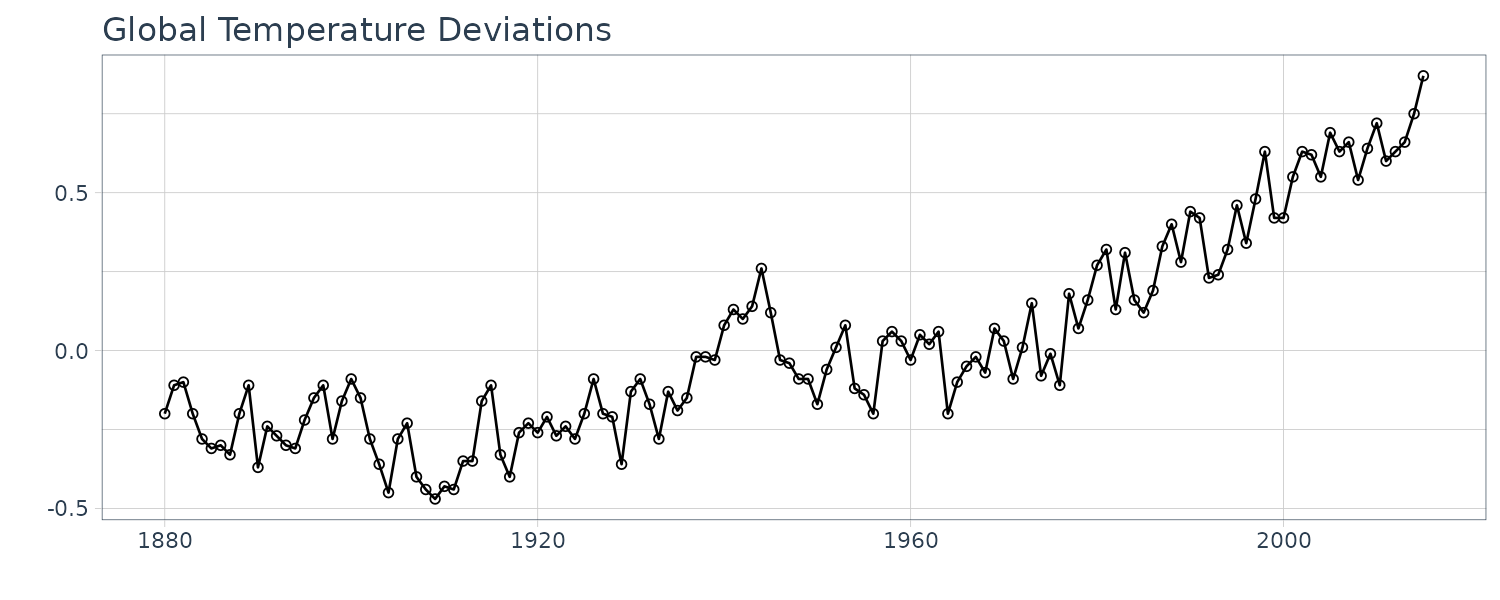
Global Warming
Global mean land-ocean temperature index from 1880 to 2015, with base period 1951-1980. The index is computed as deviation from the 1951-1980 average.
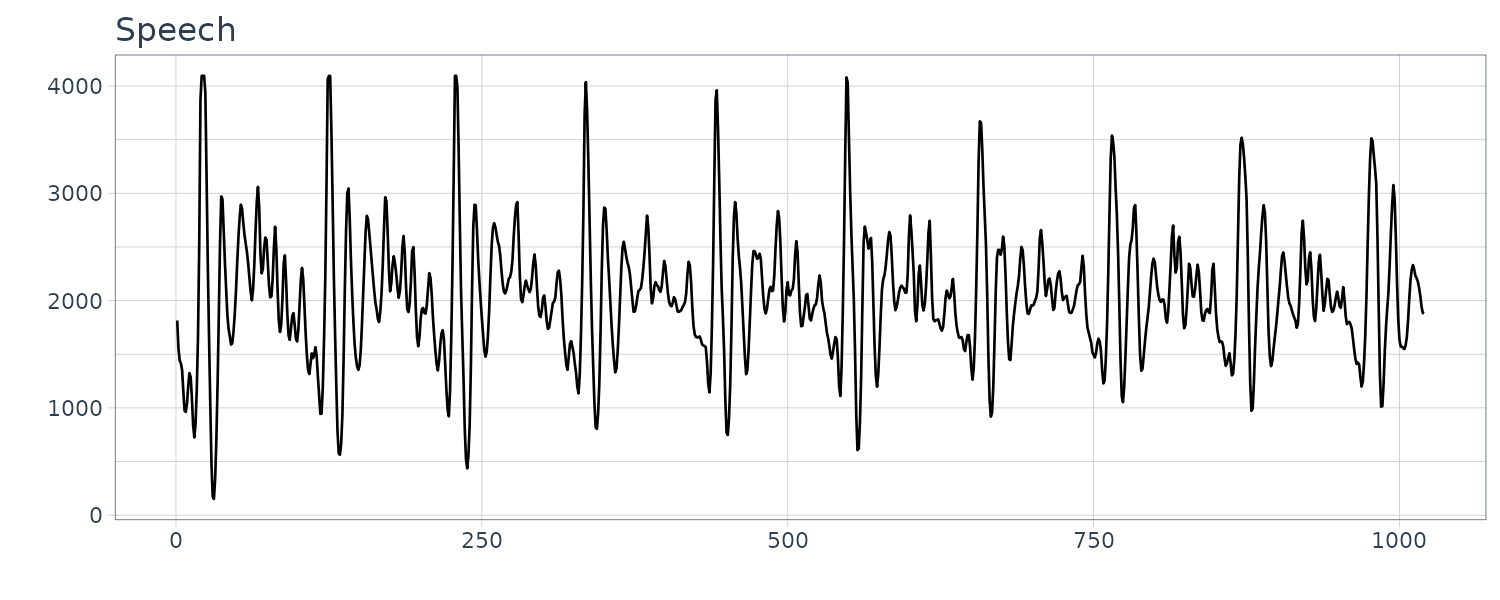
Speech Data
A 0.1 sec 1000 point sample of recorded speech for th eprhase “aahhhh”.
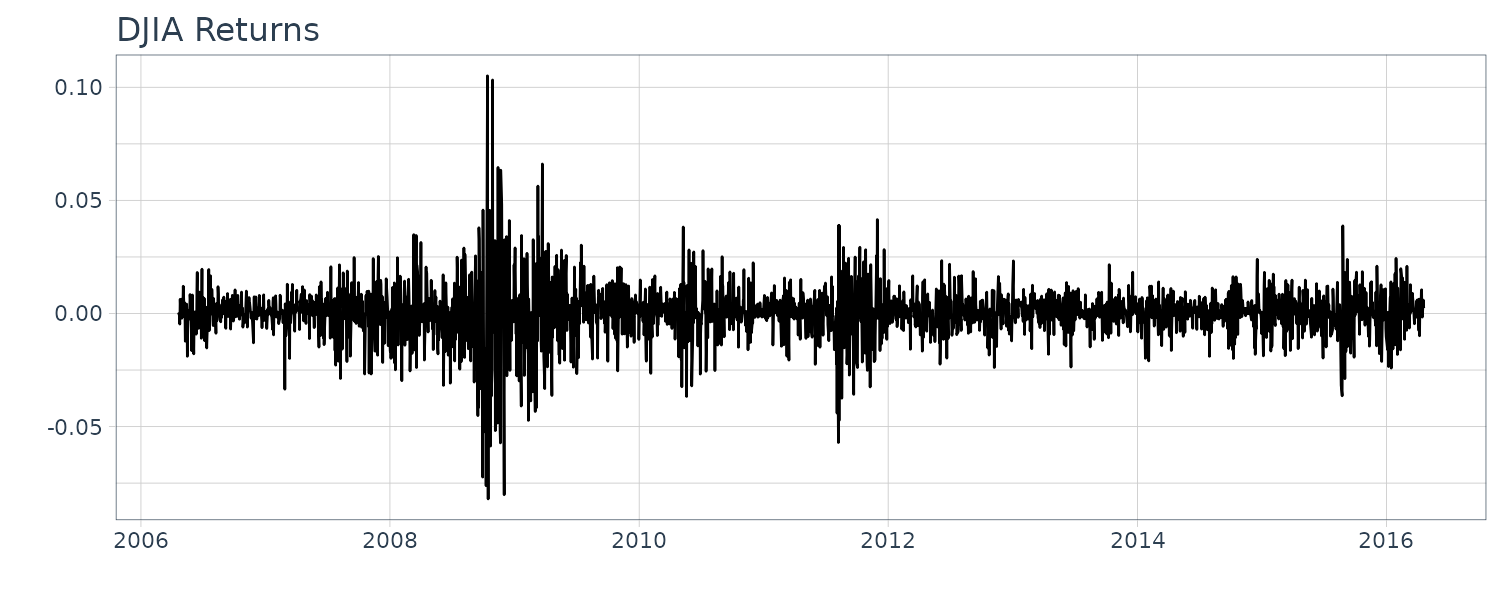
Dow Jones Industrial Average (DJIA)
Daily returns of the DJIA index from April 20, 2006 to April 20, 2016.
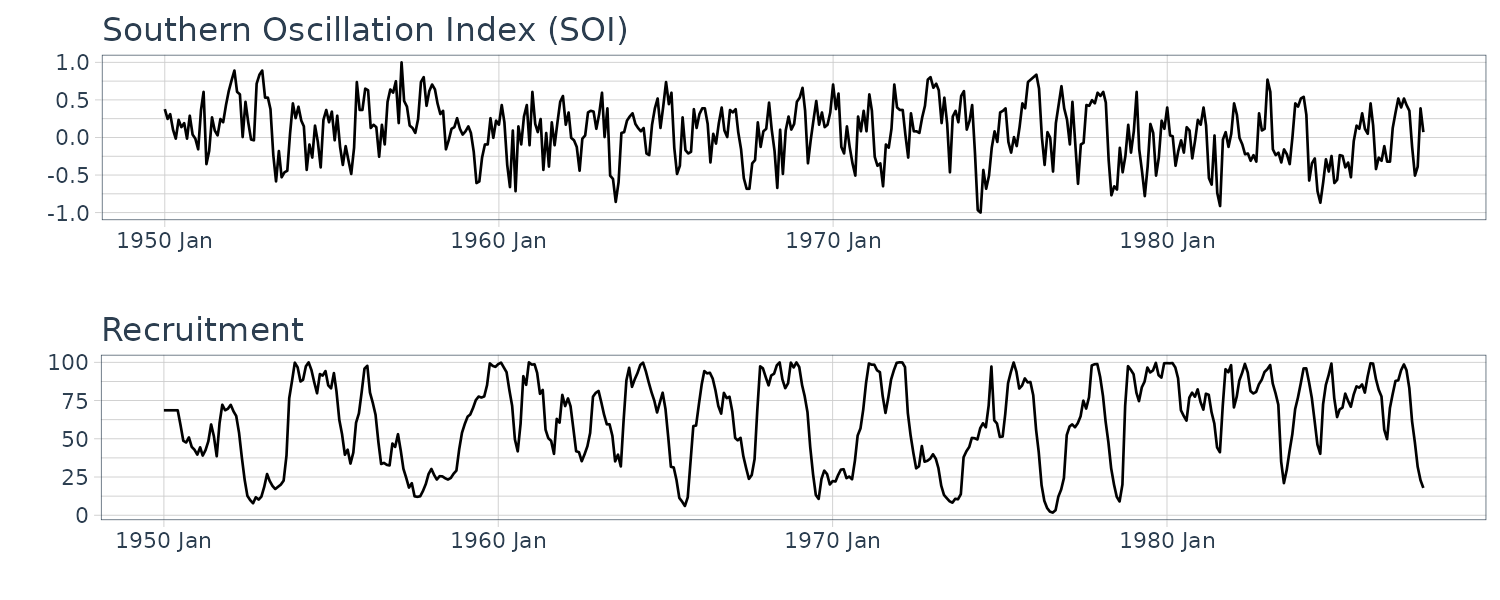
El Niño and Fish Population
Monthly values of the Southern Oscillation Index (SOI) and associated Recruitment (number of new fish) index ranging over the years 1950-1987. SOI measures changes in air pressure.
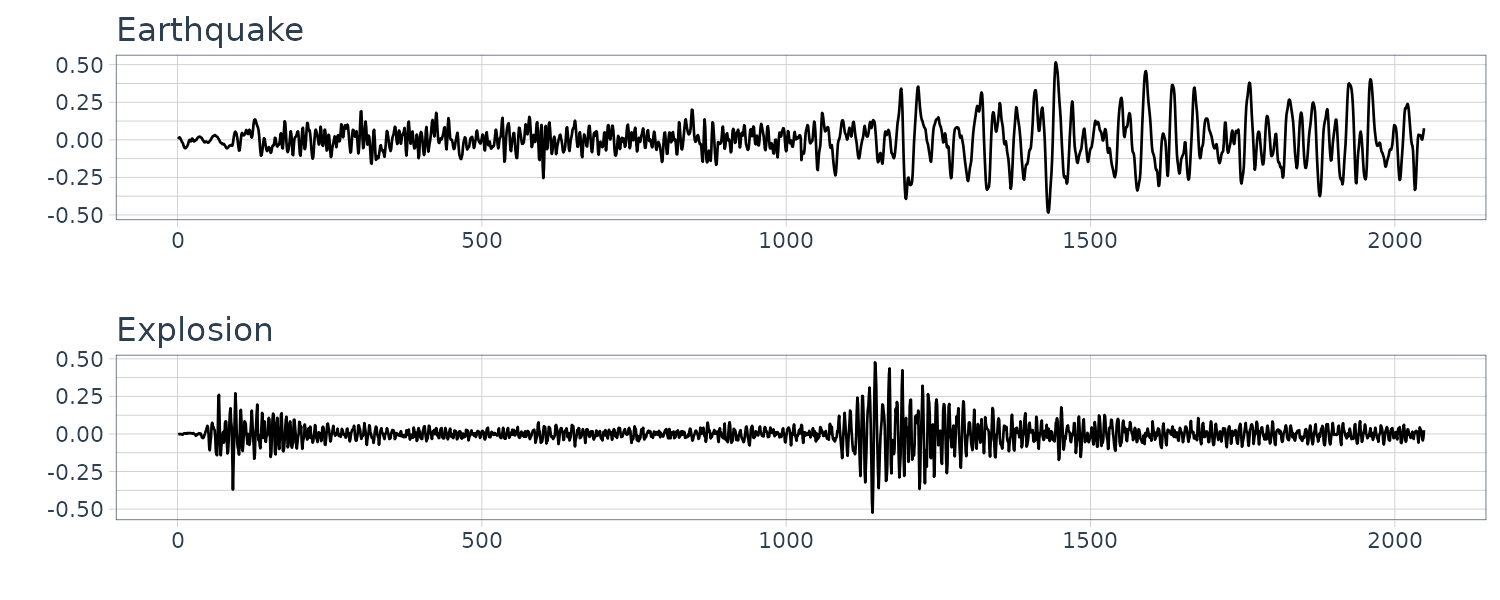
Earthquakes and Explosions
Seismic recording of an earthquake and explosion.
fMRI Imagining
Data is collected from various locations in the brain via Functional Magnetic Reasonance Imaging. A stimulus was applied for 32s and then stopped for 32 secs giving a total signal period of 64s. 1 observation is taken every 2s for 256s (n = 128).
Autocovariance
The autocovariance function is defined as:
\[\begin{aligned} \gamma_{x}(s, t) &= \mathrm{cov}(x_{s}, x_{t})\\ &= E[(x_{s} - \mu_{s})(x_{t} - \mu_{t})] \end{aligned}\]Autocovariance function measures the linear dependence between two points in time. Smooth series have large autocovariance function even when \(s, t\) are far apart, whereas choppy series tend to have autocovariance function near 0.
If the random variables are linear combinations of \(X_{j}\) and \(Y_{k}\):
\[\begin{aligned} X &= \sum_{j=1}^{m}a_{j}X_{j}\\ Y &= \sum_{k = 1}^{r}b_{k}Y_{k}\\ \mathrm{cov}(X, Y) &= E\Big[\sum_{j=1}^{m}a_{j}X_{j}\sum_{k = 1}^{r}b_{k}Y_{k}\Big]\\ &= \sum_{j=1}^{m}\sum_{k = 1}^{r}a_{j}b_{k}E[X_{j}Y_{k}]\\ &= \sum_{j = 1}^{m}\sum_{k = 1}^{r}a_{j}b_{k}\mathrm{cov}(X_{j}, Y_{k}) \end{aligned}\]If \(x_{s}, x_{t}\) are bivariate normal, \(\gamma_{x}(s, t) = 0\) implies independence as well.
And the variance:
\[\begin{aligned} \gamma_{x}(t, t) &= E[(x_{t} - \mu_{t})^{2}]\\ &= \mathrm{var}(x_{t}) \end{aligned}\]The variance of a linear combination of \(x_{t}\) can be represented as sum of autocovariances:
\[\begin{aligned} \mathrm{var}(a_{1}x_{1} + \cdots + a_{n}x_{n}) &= \mathrm{cov}(a_{1}x_{1} + \cdots + a_{n}x_{n}, a_{1}x_{1} + \cdots + a_{n}x_{n})\\ &= \sum_{j= 1}^{n}\sum_{k = 1}^{n}a_{j}a_{k}\mathrm{cov}(x_{j}, x_{k})\\ &= \sum_{j= 1}^{n}\sum_{k = 1}^{n}a_{j}a_{k}\gamma(j - k) \end{aligned}\]Note that:
\[\begin{aligned} \gamma(h) &= \gamma(-h) \end{aligned}\]The autocorrelation function (ACF) is defined as:
\[\begin{aligned} \rho(s, t) &= \frac{\gamma(s, t)}{\sqrt{\gamma(s, s)\gamma(t, t)}} \end{aligned}\]The cross-covariance function between two time series, \(x_{t}\) and \(y_{t}\):
\[\begin{aligned} \gamma_{xy}(s, t) &= \mathrm{cov}(x_{s}, y_{t})\\ &= E[(x_{s} - \mu_{xs})(y_{t} - \mu_{yt})] \end{aligned}\]And the cross-correlation function (CCF):
\[\begin{aligned} \rho_{xy}(s, t) &= \frac{\gamma_{xy}(s, t)}{\sqrt{\gamma_{x}(s, s)\gamma_{y}(t, t)}} \end{aligned}\]Estimating Correlation
In most situation, we only have a single realization (sample) to estimate the population means and covariance functions.
To estimate the mean, we use the sample mean:
\[\begin{aligned} \bar{x} &= \frac{1}{n}\sum_{t=1}^{n}x_{t} \end{aligned}\]The variance of the mean:
\[\begin{aligned} \mathrm{var}(\bar{x}) &= \mathrm{var}\Big(\frac{1}{n}\sum_{t=1}^{n}x_{t}\Big)\\ &= \sum_{j=1}^{n}\sum_{k=1}^{n}\frac{1}{n}\frac{1}{n}\mathrm{cov}(x_{j}, x_{k})\\ &= \frac{1}{n^{2}}\mathrm{cov}\Big(\sum_{t=1}^{n}x_{t},\sum_{t=1}^{n}x_{t} \Big)\\ &= \frac{1}{n^{2}}\Big(n \gamma_{x}(0) + (n-1)\gamma_{x}(1) + (n-2)\gamma_{x}(2) + \cdots + \gamma_{x}(n-1) + \\ &\ \ \ \ \ \ (n-1)\gamma_{x}(-1) + (n-2)\gamma_{x}(-2) + \cdots + \gamma_{x}(1 - n)\Big)\\ &= \frac{1}{n^{2}}\sum_{h=-n}^{n}n\Big(1 - \frac{|h|}{n}\Big)\gamma_{x}(h)\\ &= \frac{1}{n}\sum_{h=-n}^{n}\Big(1 - \frac{|h|}{n}\Big)\gamma_{x}(h) \end{aligned}\]If the process is white noise, the variance would reduce to:
\[\begin{aligned} \mathrm{var}(\bar{x}) &= \frac{1}{n}\gamma_{x}(0)\\ &= \frac{\sigma_{x}^{2}}{n} \end{aligned}\]Sample Autocovariance Function
The sample autocovariance function is defined as:
\[\begin{aligned} \hat{\gamma}(h) &= \frac{1}{n}\sum_{t=1}^{n-h}(x_{t+h} - \bar{x})(x_{t} - \bar{x}) \end{aligned}\]Note that the estimator above divides by \(n\) instead of \(n-h\). This guarantee that the variance is never negative (non-negative definite function). And because a variance is never negative, the estimate of that variance should also be non-negative:
\[\begin{aligned} \hat{\mathrm{cov}}(a_{1}x_{1} + \cdots + a_{n}x_{n}) &= \sum_{j=1}^{n}\sum_{k = 1}\hat{\gamma}(j-k) \end{aligned}\]But note that neither dividing by \(n\) or \(n-h\) result in an unbiased estimator of \(\gamma(h)\).
Similarly, the sample ACF is defined as:
\[\begin{aligned} \hat{\rho}(h) &= \frac{\hat{\gamma}(h)}{\hat{\gamma}(0)} \end{aligned}\]Using R to calculate ACF:
> ACF(soi, value) |>
slice(1:6) |>
pull(acf) |>
round(3)
[1] 0.604 0.374 0.214 0.050 -0.107 -0.187 Large-Sample Distribution of ACF
If \(x_{t}\) is white noise, then for large \(n\), the sample ACF is approximately normally distributed with 0 mean and sd:
\[\begin{aligned} \sigma_{\hat{\rho}_{x}(h)} &= \frac{1}{\sqrt{n}} \end{aligned}\]The larger the sample-size \(n\), the smaller standard deviation.
An example of ACF of speech dataset:
speech |>
ACF(value, lag_max = 250) |>
autoplot() +
xlab("") +
theme_tq() +
ggtitle("Speech")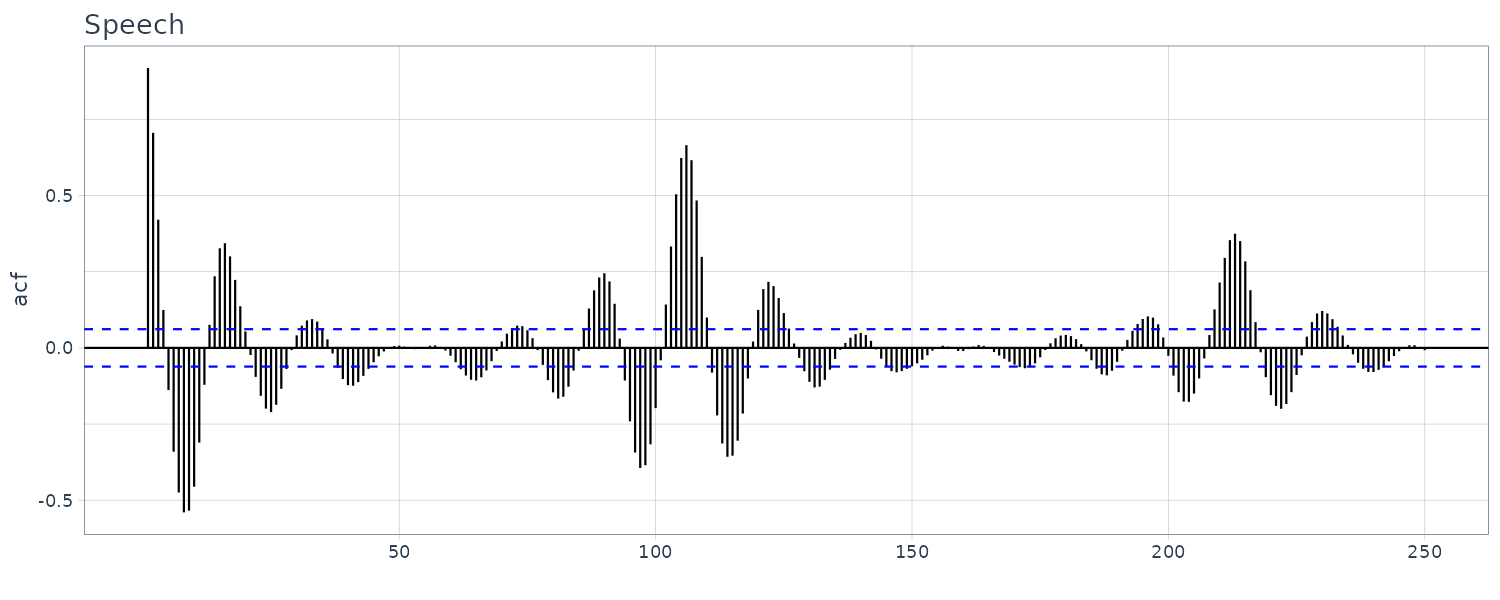
Sample Cross-Covariance Function
\[\begin{aligned} \hat{\gamma}_{xy}(h) &= \frac{1}{n}\sum_{t=1}^{n-h}(x_{t+h} - \bar{x})(y_{t} - \bar{y}) \end{aligned}\]And the sample CCF:
\[\begin{aligned} \hat{\rho}_{xy}(h) &= \frac{\hat{\rho}_{xy}(h)}{\sqrt{\hat{\gamma}_{x}(0)\hat{\gamma}_{y}(0)}} \end{aligned}\]Large-Sample Distribution of Cross-Correlation
If at least one of the processes is independent white noise:
\[\begin{aligned} \sigma_{\hat{\rho}_{xy}} &= \frac{1}{\sqrt{n}} \end{aligned}\]Prewhitening and Cross Correlation Analysis
In order to test for cross linear dependence, at least one of the series must be white noise.
To show as example, we generate two series:
\[\begin{aligned} x_{t} &= 2\mathrm{cos}\Big(2\pi \frac{t}{12}\Big) + w_{t1}\\ y_{t} &= 2\mathrm{cos}\Big(2\pi \frac{t+5}{12}\Big) + w_{t2}\\ \end{aligned}\]If you look at the CCF:
set.seed(1492)
num <- 120
t <- 1:num
dat <- tsibble(
t = t,
X = 2 * cos(2 * pi * t / 12) + rnorm(num),
Y = 2 * cos(2 * pi * (t + 5) / 12) + rnorm(num),
index = t
)
dat |>
CCF(Y, X) |>
autoplot() +
ggtitle("CCF(X, Y)") +
theme_tq()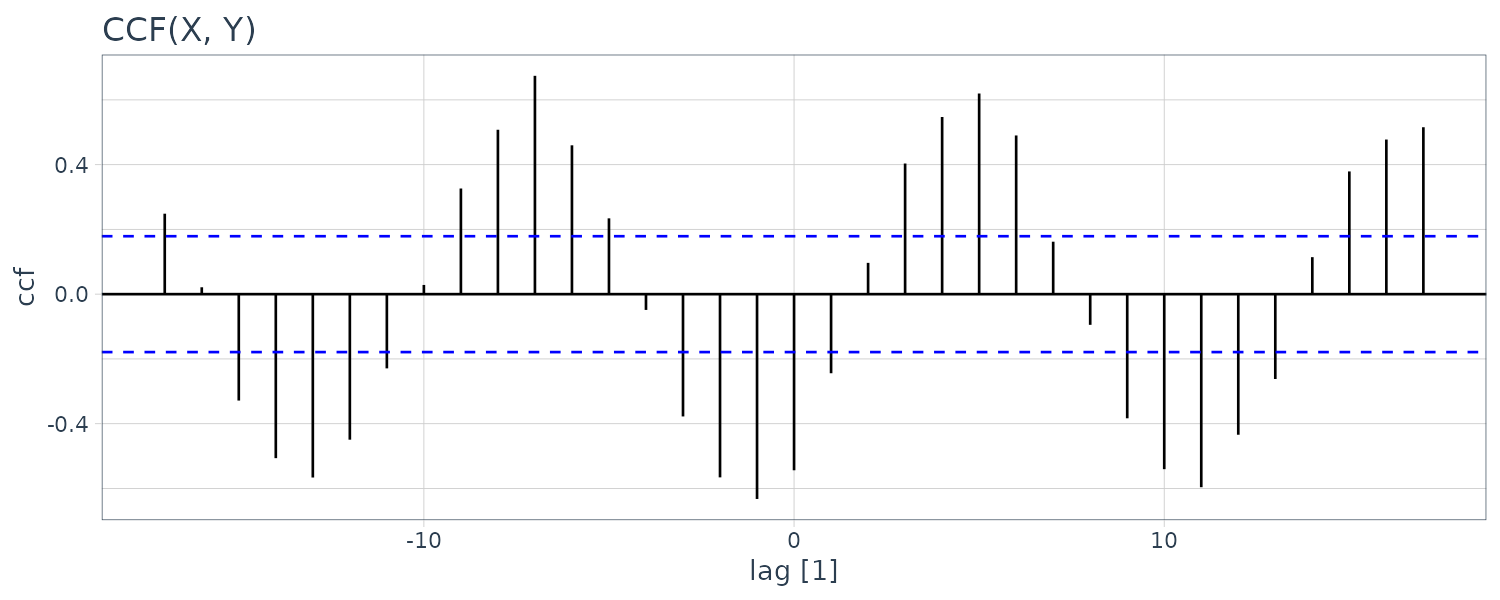
There appears to be cross-correalation between the sampe CCF although we know that the two series are independent.
By prewhitening \(y_{t}\) , we mean that the signal has been removed from the data by running a regression of \(y_{t}\) on \(\mathrm{cos}(2\pi t), \mathrm{sin}(2\pi t)\) and then assigning \(\tilde{y}_{t} = y_{t} - \hat{y}_{t}\). Doing this in R:
dat <- dat |>
mutate(
Yw = resid(
lm(
Y ~ cos(2 * pi * t / 12) +
sin(2 * pi * t / 12),
na.action = NULL
)
)
)
dat |>
CCF(Yw, X) |>
autoplot() +
ggtitle("CCF(X, Y)") +
theme_tq()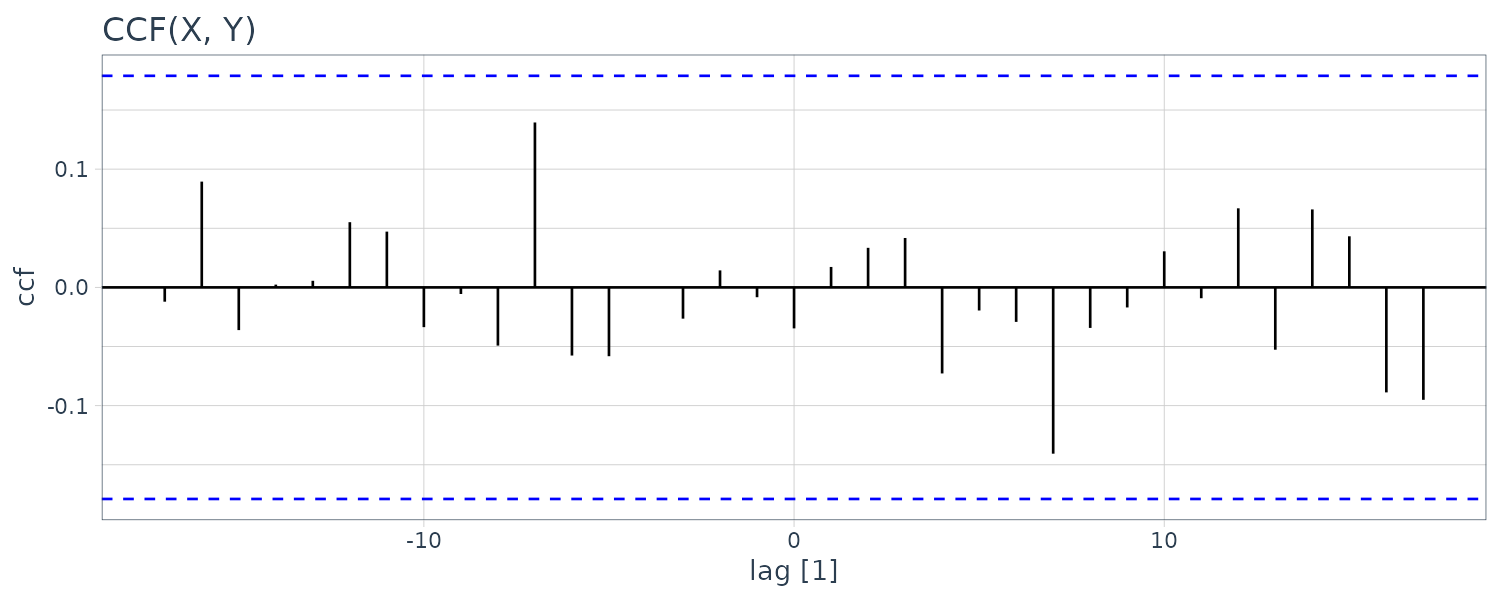
We can see that the cross-correlation is now insignificant.
Stationary Time Series
A strictly stationary time series has the same probability distribution when shifted by \(h\):
\[\begin{aligned} P(x_{t1} \leq c_{1}, \cdots, x_{tk} \leq c_{k}) &= P(x_{t1 + h} \leq c_{1}, \cdots, x_{tk + h} \leq c_{k})\\ k &= 1, 2, \cdots \end{aligned}\]Usually the strictly stationary condition is too imposing and a weaker version that only impose the first two moments of a series is known as a “weakly statoionary” time series such that:
\[\begin{aligned} E[x_{t}] &= \mu_{t}\\ &= \mu\\ \gamma(t + h, t) &= \mathrm{cov}(x_{t + h}, x_{t})\\ &= \mathrm{cov}(x_{h}, x_{0})\\ &= \gamma(h, 0)\\ &= \gamma(h) \end{aligned}\]In other words, the autocovariance function can be written as:
\[\begin{aligned} \gamma(h) &= \mathrm{cov}(x_{t+h}, x_{t})\\ &= E[(x_{t+h} - \mu)(x_{t} - \mu)] \end{aligned}\]And the ACF:
\[\begin{aligned} \rho(h) &= \frac{\gamma(t+h, t)}{\sqrt{\gamma(t+h, t+h)\gamma(t, t)}}\\[5pt] &= \frac{\gamma(h)}{\gamma(0)} \end{aligned}\]Jointly Stationary
Two stationary time series \(x_{t}\) and \(y_{t}\) are said to be jointly stationary if the cross-covariance function is a function only of lag h:
\[\begin{aligned} \gamma_{xy}(h) &= \mathrm{cov}(x_{t+h}, y_{t})\\ &= E[(x_{t+h} - \mu_{x})(y_{t} - \mu_{y})] \end{aligned}\]The CCF:
\[\begin{aligned} \rho_{xy}(h) &= \frac{\gamma_{xy}(h)}{\sqrt{\gamma_{x}(0)\gamma_{y}(0)}} \end{aligned}\]In general,
\[\begin{aligned} \rho_{xy}(h) &\neq \rho_{xy}(-h)\\ \rho_{xy}(h) &= \rho_{yx}(-h) \end{aligned}\]For example, if:
\[\begin{aligned} x_{t} &= w_{t} + w_{t-1}\\ y_{t} &= w_{t} - w_{t-1}\\ x_{t+1} &= w_{t+1} + w_{t}\\ y_{t+1} &= w_{t+1} - w_{t} \end{aligned}\] \[\begin{aligned} \gamma_{x}(0) &= 2\sigma_{w}^{2}\\ \gamma_{y}(0) &= 2\sigma_{w}^{2}\\ \gamma_{x}(1) &= \sigma_{w}^{2}\\ \gamma_{y}(1) &= E[y_{t+1}y_{t}]\\ &= E[(w_{t+1} - w_{t})(w_{t} - w_{t-1})]\\ &= 0 - 0 - E[w_{t}w_{t}] + 0\\ &= -\sigma_{w}^{2} \end{aligned}\]We can show that the autocovariance function depend only on the lag \(h\) and hence jointly stationary:
\[\begin{aligned} \gamma_{xy}(1) &= \mathrm{cov}(x_{t+1}, y_{t})\\ &= \mathrm{cov}(w_{t+1} + w_{t}, w_{t} - w_{t-1})\\ &= E[(w_{t+1} + w_{t})(w_{t} - w_{t-1})]\\ &= 0 + 0 + E[w_{t}w_{t}] - 0\\ &= \sigma_{w}^{2} \end{aligned}\]CCF:
\[\begin{aligned} \sqrt{\gamma_{x}(0)\gamma_{y}(0)} &= \sqrt{2\sigma_{w}^{2}\times 2\sigma_{w}^{2}}\\ &= 2\sigma_{w}^{2} \end{aligned}\] \[\begin{aligned} \rho_{xy}(h) &= \begin{cases} 0 & h = 0\\ \frac{1}{2} & h = 1\\ -\frac{1}{2} & h = -1\\ 0 & |h| \geq 2 \end{cases} \end{aligned}\]Another example of cross-correlation where one series lead/lag another series. For the following model:
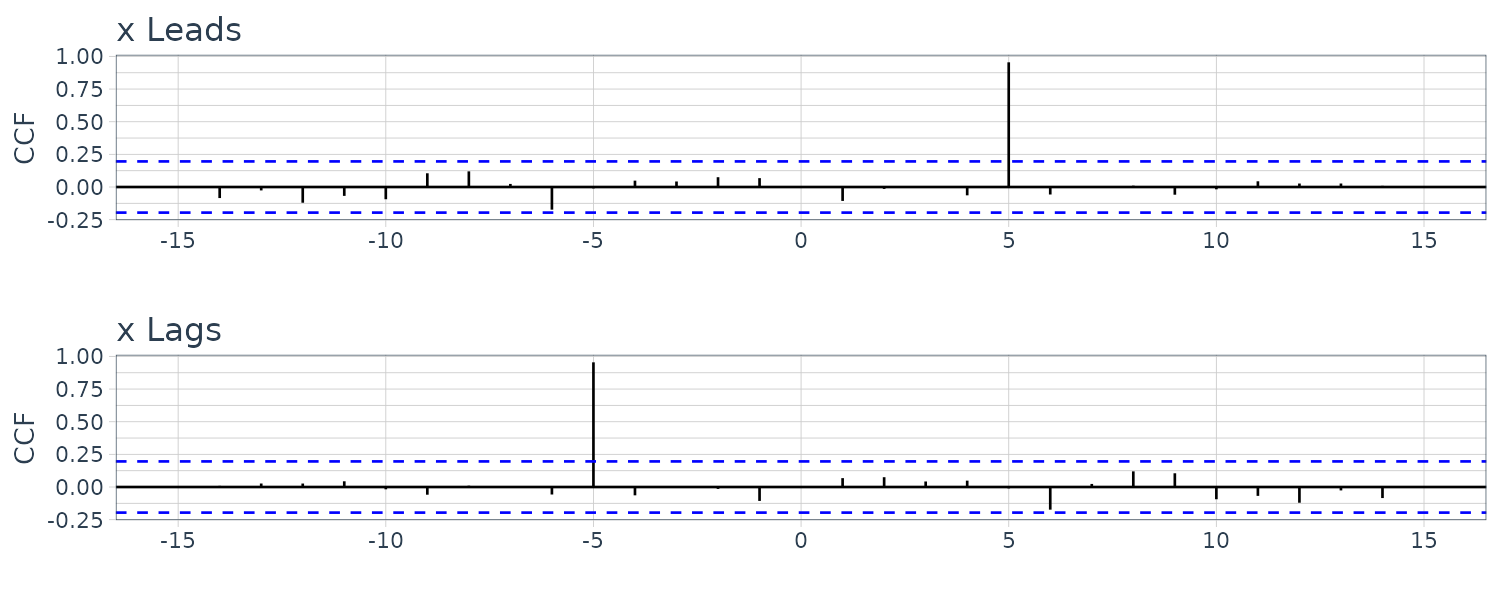
\[\begin{aligned} y_{t} &= Ax_{t-l} + w_{t} \end{aligned}\]If \(l > 0\), \(x_{t}\) is said to lead \(y_{t}\) and if \(l < 0\), \(x_{t}\) is said to lag \(y_{t}\).
Assuming \(w_{t}\) is uncorrelated with the \(x_{t}\) series, the cross-covariance function:
\[\begin{aligned} \gamma_{yx}(h) &= \mathrm{cov}(y_{t+h}, x_{t})\\ &= \mathrm{cov}(A x_{t+h - l} + w_{t+h}, x_{t})\\ &= \mathrm{cov}(A x_{t+h - l}, x_{t})\\ &= A\gamma_{x}(h - l) \end{aligned}\]\(\gamma_{x}(h - l)\) will peak when \(h - l = 0\):
\[\begin{aligned} \gamma_{x}(h - l) &= \gamma_{x}(0) \end{aligned}\]If \(x_{t}\) leads \(y_{t}\), the peak will be on the positive side and vice versa.
x <- rnorm(100)
dat <- tsibble(
t = 1:100,
x = x,
y1 = lead(x, 5),
y2 = lag(x, 5),
index = t
)
plot_grid(
dat |>
CCF(y1, x, lag_max = 15) |>
autoplot() +
ylab("x Leads")
xlab("") +
theme_tq(),
dat |>
CCF(y2, x, lag_max = 15) |>
autoplot() +
ylab("x Lags")
xlab("") +
theme_tq(),
ncol = 1
)
Linear Process
A linear process, \(x_{t}\), is defined to be a linear combination of white noise variates \(w_{t}\):
\[\begin{aligned} x_{t} &= \mu + \sum_{j = -\infty}^{\infty}\psi_{j}w_{t-j} \end{aligned}\] \[\begin{aligned} \sum_{j=-\infty}^{\infty}|\psi_{j}| &< \infty \end{aligned}\]The autocovariance can be shown to be:
\[\begin{aligned} \gamma_{x}(h) &= \sigma_{w}^{2}\sum_{j=-\infty}^{\infty}\psi_{j+h}\psi_{j} \end{aligned}\]For a causal linear process, the processes do not depend on the future and we will have:
\[\begin{aligned} \psi_{j} &= 0\\ j &< 0 \end{aligned}\]Gaussian Process
A process, \(\{x_{t}\}\), is said to be a Gaussian process if the n-dimensional \(\mathbf{x} = (x_{t1}, x_{t2}, \cdots, x_{tn})\) have a multivariate normal distribution.
Defining the mean and variance to be:
\[\begin{aligned} E[\mathbf{x}] &\equiv \boldsymbol{\mu}\\ &= \begin{bmatrix} \mu_{t1}\\ \mu_{t2}\\ \vdots\\ \mu_{tn} \end{bmatrix}\\[5pt] \mathrm{var}(\mathbf{x}) &\equiv \boldsymbol{\Gamma}\\ &= \{\gamma(t_{i}, t_{j}); i, j = 1, \cdots, n\} \end{aligned}\]The multivariate normal density function can then be written as:
\[\begin{aligned} f(\mathbf{x}) &= (2\pi)^{-\frac{n}{2}}|\boldsymbol{\Gamma}|^{-\frac{1}{2}}e^{\frac{1}{2}(\mathbf{x} - \boldsymbol{\mu})^{T}\boldsymbol{\Gamma}^{-1}(\mathbf{x}- \boldsymbol{\mu})} \end{aligned}\]If the Gaussian time series, \(x_{t}\), is weakly stationary, then \(\mu_{t}\) is constant and:
\[\begin{aligned} \gamma(t_{i}, t_{j}) = \gamma(|t_{i} - t_{j}|) \end{aligned}\]So that the vector \(\boldsymbol{\mu}\) and matrix \(\boldsymbol{\Gamma}\) are independent of time and consist of constant values.
Note that it is not enough for the marginal distributions to be Gaussian in order for the joint distribution to be Gaussian.
Wold Decomposition
Wold Decomposition states that a stationary non-deterministic time series is a causal linear process:
\[\begin{aligned} x_{t} &= \mu + \sum_{j = 0}^{\infty}\psi_{j}w_{t-j} + v_{t}\\ \sum_{j=0}^{\infty}|\psi_{j}| &< \infty\\ \psi_{0} &= 1 \end{aligned}\]If the linear process is Gaussian, then:
\[\begin{aligned} w_{t} &\sim \text{iid } N(0, \sigma_{w}^{2})\\ \text{cov}(w_{s}, v_{t}) &= 0 \end{aligned}\] \[\begin{aligned} \forall s, t \end{aligned}\]Time Series Statistical Models
White Noise
A collection of uncorrelated random variables with mean 0 and finite variance. Additionally, we require the random variables to be iid. If the RV is further Gaussian then:
\[\begin{aligned} w_{t} \sim N(0, \sigma_{\omega}^{2}) \end{aligned}\]Autocovariance function:
\[\begin{aligned} \gamma_{w}(s, t) &= \mathrm{cov}(w_{s}, w_{t})\\ &= \begin{cases} \sigma_{w}^{2} & s = t\\ 0 & s \neq t \end{cases} \end{aligned}\]Because white noise is weakly stationary, we can represent it in terms of lag \(h\):
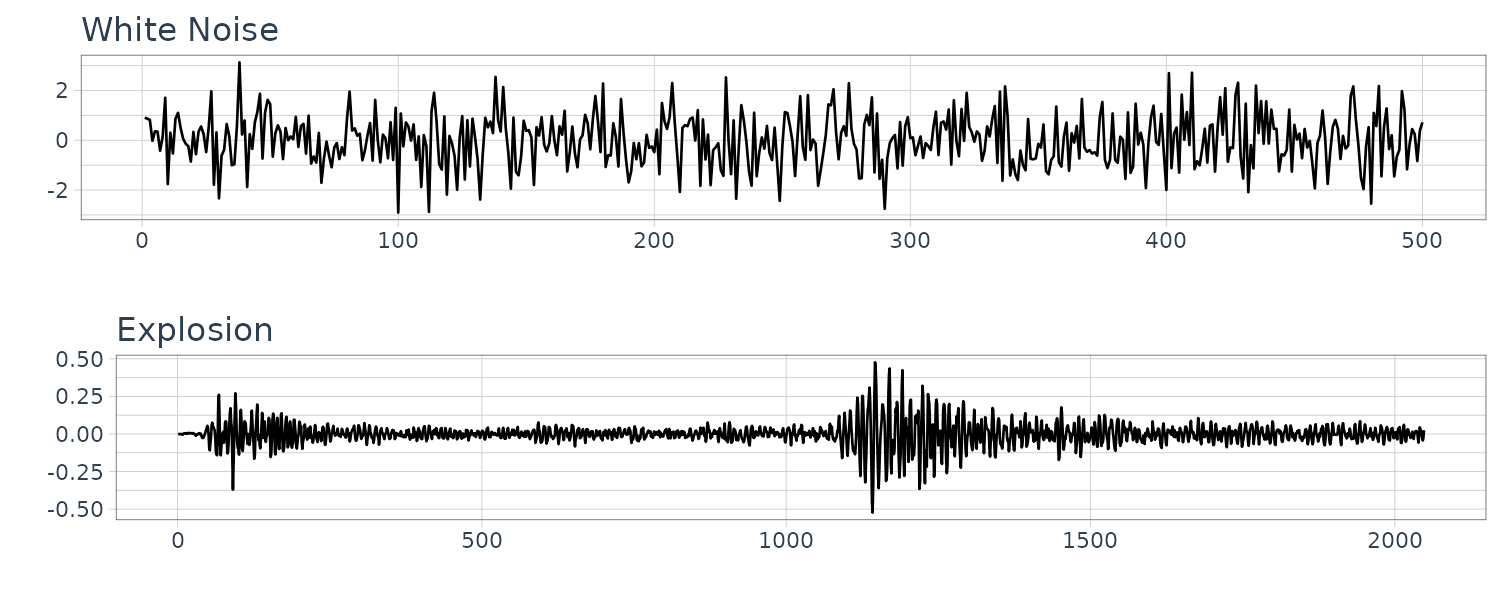
\[\begin{aligned} \gamma_{w}(h) &= \mathrm{cov}(w_{t + h}, w_{t})\\ &= \begin{cases} \sigma_{w}^{2} & h = 0\\ 0 & h \neq 0 \end{cases} \end{aligned}\]The explosion series bears a slight resemblance to white noise:
dat <- tsibble(
w = rnorm(500, 0, 1),
t = 1:500,
index = t
)
plot_grid(
dat |>
autoplot(w) +
xlab("") +
ggtitle("White Noise") +
theme_tq(),
dat |>
autoplot(v) +
xlab("") +
ggtitle("Explosion") +
theme_tq(),
ncol = 1
)
Moving Averages
To introduce serial correlation into the time series, we can replace the white noise series by a moving average that smooths out the series:
\[\begin{aligned} \nu_{t} = \frac{1}{3}(w_{t-1} + w_{t} + w_{t+1}) \end{aligned}\]And the mean:
\[\begin{aligned} \mu_{\nu t} &= E[\nu_{t}]\\ &= \frac{1}{3}\Big(E[w_{t-1} + w_{t} + w_{t+1}]\Big)\\ &= \frac{1}{3}\Big(E[w_{t-1}] + E[w_{t}] + E[w_{t+1}]\Big)\\ &= 0 \end{aligned}\]Autocovariance function:
\[\begin{aligned} \gamma_{\nu}(s, t) = &\ \mathrm{cov}(\nu_{s}, \nu_{t})\\ = &\ \frac{1}{9}\mathrm{cov}(w_{s-1} + w_{s} + w_{s+1}, w_{t-1} + w_{t} + w_{t+1})\\ = &\ \frac{1}{9}\Big( \mathrm{cov}(w_{s-1}, w_{t-1}) + \mathrm{cov}(w_{s-1}, w_{t}) + \mathrm{cov}(w_{s-1}, w_{t+1}) +\\ &\ \ \ \mathrm{cov}(w_{s}, w_{t-1}) + \mathrm{cov}(w_{s}, w_{t}) + \mathrm{cov}(w_{s}, w_{t+1}) +\\ &\ \ \ \mathrm{cov}(w_{s+1}, w_{t-1}) + \mathrm{cov}(w_{s+1}, w_{t}) + \mathrm{cov}(w_{s+1}, w_{t+1}) \Big) \end{aligned}\] \[\begin{aligned} \gamma_{\nu}(t, t) &= \frac{1}{9}\Big( \mathrm{cov}(w_{t-1}, w_{t-1}) + \mathrm{cov}(w_{t}, w_{t}) + \mathrm{cov}(w_{t+1}, w_{t})\Big)\\ &= \frac{3}{9}\sigma_{w}^{2} \end{aligned}\] \[\begin{aligned} \gamma_{\nu}(t + 1, t) &= \frac{1}{9}\Big[ \mathrm{cov}(w_{t}, w_{t}) + \mathrm{cov}(w_{t+1}, w_{t})\Big]\\ &= \frac{2}{9}\sigma_{w}^{2} \end{aligned}\]In summary:
\[\begin{aligned} \gamma_{\nu}(s, t) &= \begin{cases} \frac{3}{9}\sigma_{w}^{2} & s = t\\ \frac{2}{9}\sigma_{w}^{2} & |s-t| = 1\\ \frac{1}{9}\sigma_{w}^{2} & |s-t| = 2\\ 0 & |s - t| > 2 \end{cases} \end{aligned}\]And in terms of lags:
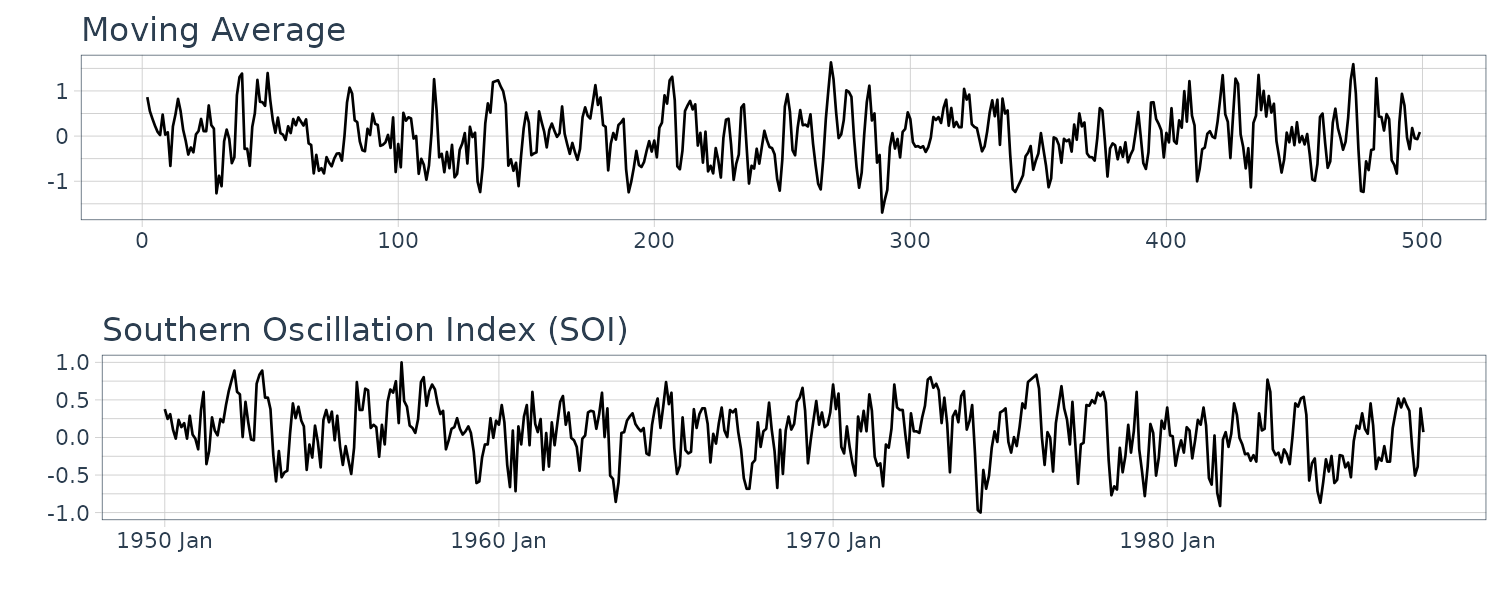
\[\begin{aligned} \gamma_{\nu}(h) &= \begin{cases} \frac{3}{9}\sigma_{w}^{2} & h = 0\\ \frac{2}{9}\sigma_{w}^{2} & h = \pm 1\\ \frac{1}{9}\sigma_{w}^{2} & h = \pm 2\\ 0 & |h| > 2 \end{cases}\\ \rho_{\nu}(h) &= \begin{cases} 1 & h = 0\\ \frac{2}{3} & h = \pm 1\\ \frac{1}{3} & h = \pm 2\\ 0 & |h| > 2 \end{cases} \end{aligned}\]Note that the autocovariance function depends only on the lag and decreases and completely disappear after 3 lags.
Note the absence of any periodicity in the series. We can see the resemblance to the SOI series:
dat$v <- stats::filter(
dat$w,
sides = 2,
filter = rep(1 / 3, 3)
)
Autoregressions
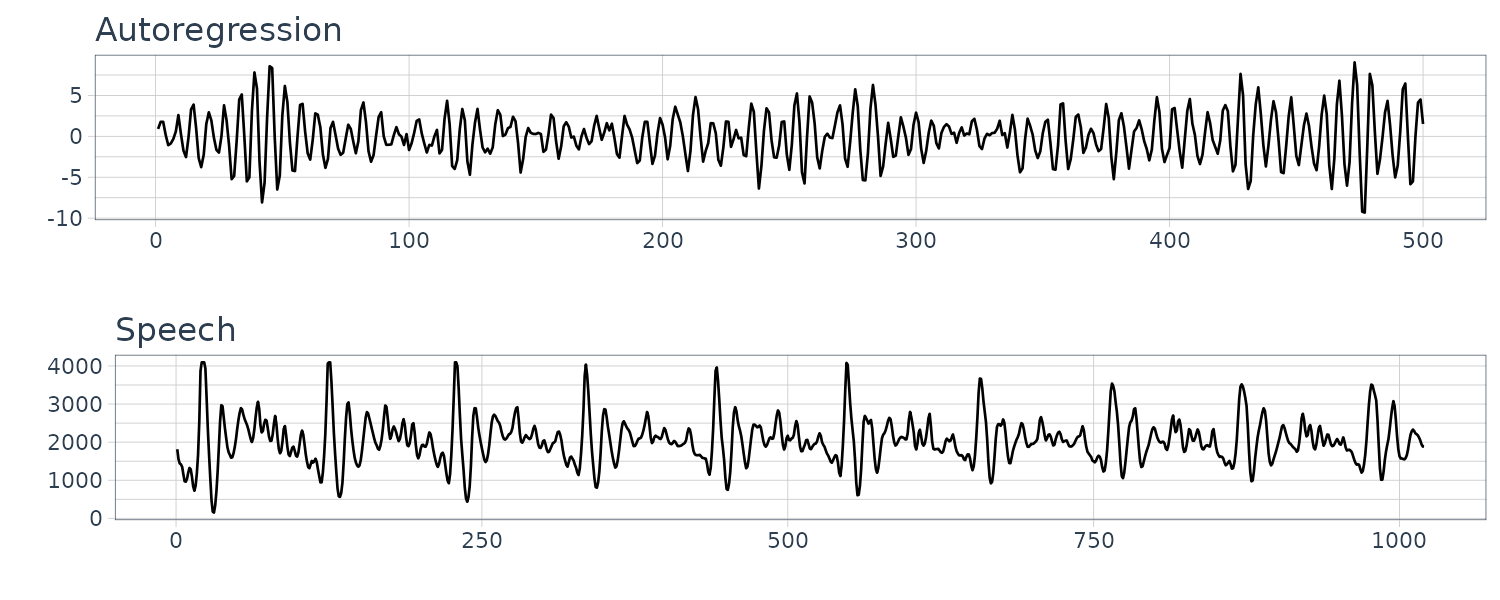
To generate a somewhat periodic behavior, we can turn to autoregression model. For example:
\[\begin{aligned} x_{t} &= x_{t-1} - 0.9x_{t-2} + w_{t} \end{aligned}\]We can see the resemblance to the speech data:
dat$x <- stats::filter(
dat$w,
filter = c(1, -0.9),
method = "recursive"
)
Random Walk with Drift
\[\begin{aligned} x_{t} &= \delta + x_{t-1} + w_{t}\\ x_{0} &= 0 \end{aligned}\]The above is the same as a cumulative sum of white noise variates:
\[\begin{aligned} x_{t} &= \delta t + \sum_{j=1}^{t}w_{j} \end{aligned}\]And the mean:
\[\begin{aligned} \mu_{xt} &= E[x_{t}]\\ &= \delta t + \sum_{j=1}^{t}E[w_{j}]\\ &= \delta t \end{aligned}\]Autocovariance function:
\[\begin{aligned} \gamma_{x}(s, t) &= \mathrm{cov}(x_{s}, x_{t})\\ &= \mathrm{cov}\Big( \sum_{j=1}^{s}w_{j}, \sum_{k = 1}^{t}w_{k} \Big)\\ &= \mathrm{min}\{s, t\}\sigma_{w}^{2} \end{aligned}\]Because \(w_{t}\) are uncorrelated, and thus only the overlapped variances are added. Note that the autocovariance function depends on particular values of \(s\) and \(t\), and thus not stationary.
For the variance:
\[\begin{aligned} \mathrm{var}(x_{t}) &= \gamma_{x}(t, t)\\ &= t\sigma_{w}^{2} \end{aligned}\]Note that the variance increases without bound as time \(t\) increases.
And note the resemblance to Global Temperature Deviations:
dat$xd <- cumsum(dat$w + 0.2) 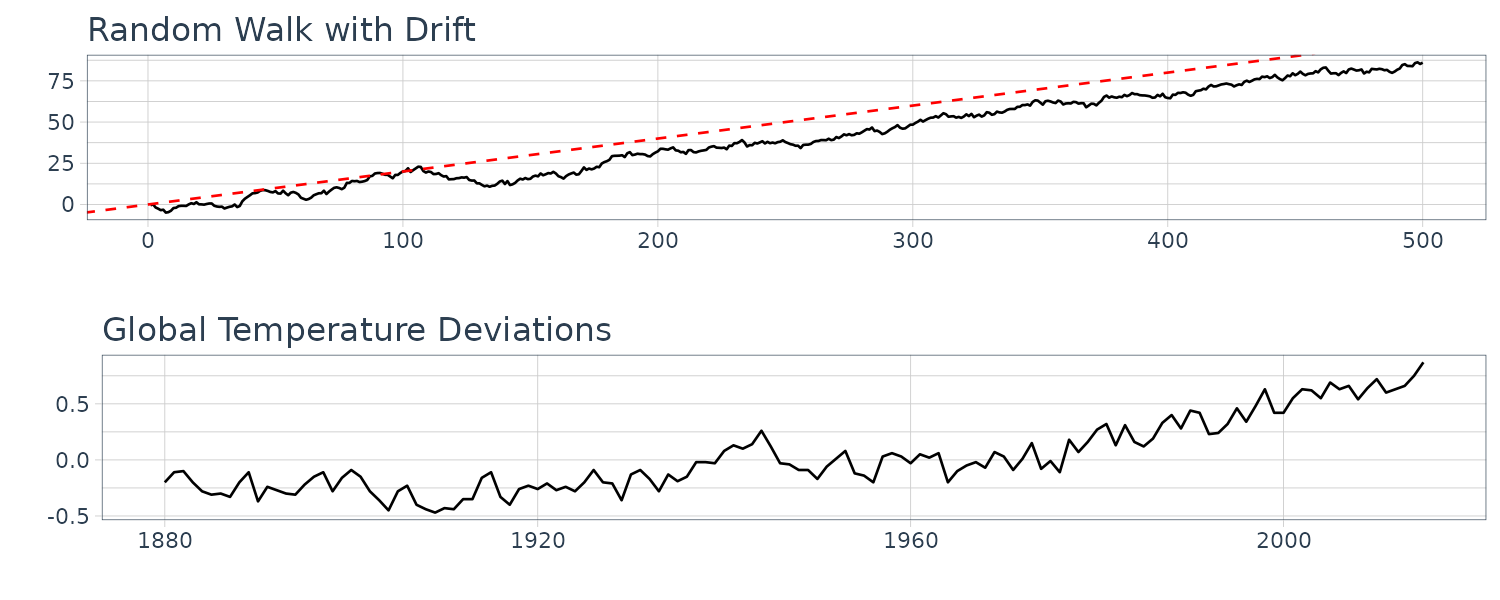
Trend Stationarity
Consider the model:
\[\begin{aligned} x_{t} &= \alpha + \beta t + y_{t} \end{aligned}\]Where \(y_{t}\) is stationary. Then the mean:
\[\begin{aligned} \mu_{x, t} &= E[x_{t}]\\ &= \alpha + \beta t + \mu_{y} \end{aligned}\]Which is not independent of time. However, for the autocovariance function:
\[\begin{aligned} \gamma_{x}(h) &= \mathrm{cov}(x_{t+h}, x_{t})\\ &= E[(x_{t+h} - \mu_{x, t+h})(x_{t} - \mu_{x,t})]\\ &= E[(y_{t+h} - \mu_{y})(y_{t} - \mu_{y})]\\ &= \gamma_{y}(h) \end{aligned}\]Is independent of time. In other words, after removing the trend, the model is stationary, or the model is considered stationary around a linear trend.
Signal in Noise
Consider the model:
\[\begin{aligned} x_{t} &= 2 \mathrm{cos}\Big(2\pi \frac{t + 15}{50}\Big) + w_{t} \end{aligned}\]And the mean:
\[\begin{aligned} \mu_{xt} &= E[x_{t}]\\ &= E\Big[2\mathrm{cos}\Big(2\pi \frac{t+15}{50}\Big) + w_{t}\Big]\\ &= 2\mathrm{cos}\Big(2\pi \frac{t+15}{50}\Big) + E[w_{t}]\\ &= 2\mathrm{cos}\Big(2\pi \frac{t+15}{50}\Big) \end{aligned}\]Note that any sinusoidal wave can be written as:
\[\begin{aligned} A \mathrm{cos}(2\pi \omega t + \phi) \end{aligned}\]In the example:
\[\begin{aligned} A &= 2\\ \omega &= \frac{1}{50}\\ \phi &= \frac{2\pi 15}{50}\\ &= 0.6 \pi \end{aligned}\]Adding white noise to the signal:
w <- rnorm(500, 0, 1)
cs <- 2 * cos(2 * pi * 1:500 / 50 + .6 * pi)
dat <- tsibble(
t = 1:500,
cs = cs + w,
index = t
)Note the similarity with fMRI series:

Classical Regression
In a classical linear regression model:
\[\begin{aligned} x_{t} &= \beta_{0} + \beta_{1}z_{t1} + \cdots + \beta_{q}z_{tq} + w_{t} \end{aligned}\]For time series regression, it is rarely the case where the residual is white noise.
For example, consider the monthly price (per pound) of a chicken for 180 months:
chicken <- as_tsibble(chicken)
chicken <- tsibble(
t = 1:nrow(chicken),
value = chicken$value,
index = t
)
> chicken
# A tsibble: 180 x 2 [1]
t value
<int> <dbl>
1 1 65.6
2 2 66.5
3 3 65.7
4 4 64.3
5 5 63.2
6 6 62.9
7 7 62.9
8 8 62.7
9 9 62.5
10 10 63.4
# ℹ 170 more rows
# ℹ Use `print(n = ...)` to see more rows Linear regression model:
\[\begin{aligned} x_{t} &= \beta_{0} + \beta_{1}z_{t} + w_{t} \end{aligned}\]We would like to minimize the SSE:
\[\begin{aligned} \text{SSE} &= \sum_{t = 1}^{n}\Big(x_{t} - (\beta_{0} + \beta_{1}z_{t})^{2}\Big) \end{aligned}\]By differentiating and setting both parameters to 0, we get:
\[\begin{aligned} \hat{\beta_{1}} &= \frac{\sum_{t=1}^{n}(x_{t} - \bar{x})(z_{t} - \bar{z})}{\sum_{t=1}^{n}(z_{t} - \bar{z})}\\[5pt] \hat{\beta}_{0} &= \bar{x} - \hat{\beta}_{1}\bar{z} \end{aligned}\]Using R to fit a linear model:
fit <- lm(
value ~ t,
data = chicken
)
chicken |>
autoplot(value) +
geom_abline(
intercept = coef(fit)[1],
slope = coef(fit)[2],
col = "red"
) +
xlab("") +
ylab("") +
ggtitle("Chicken Prices") +
theme_tq()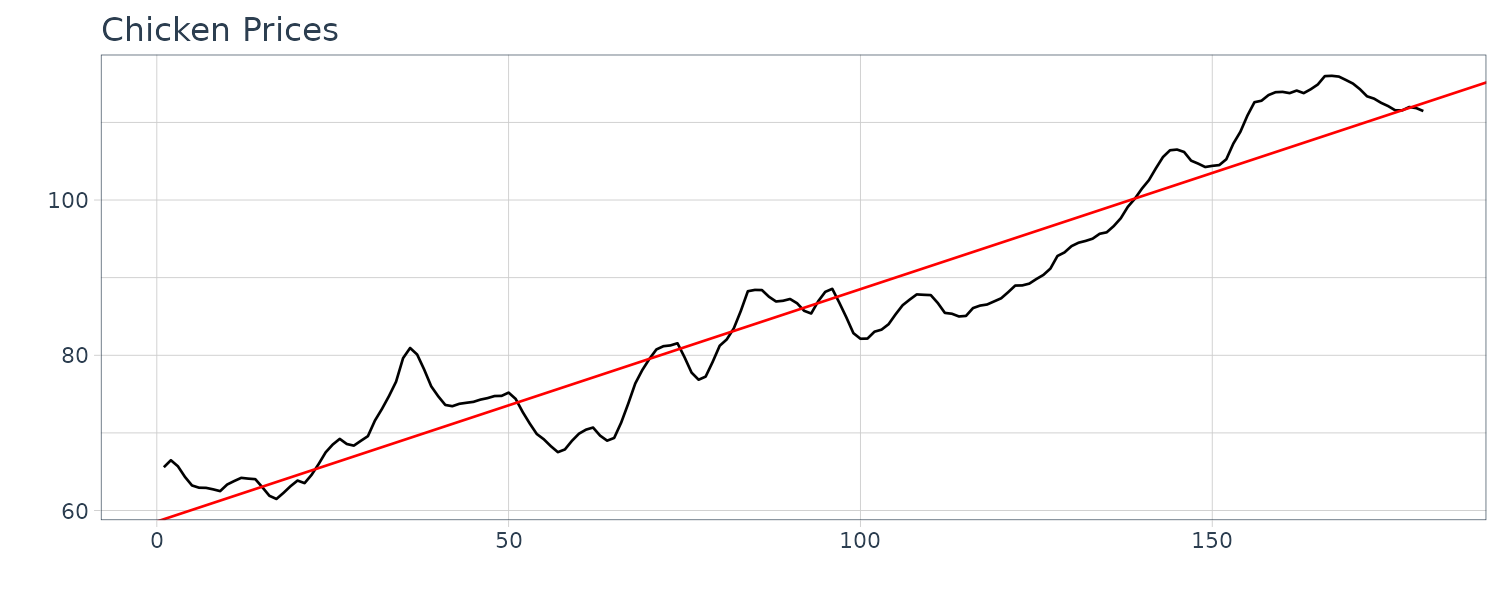
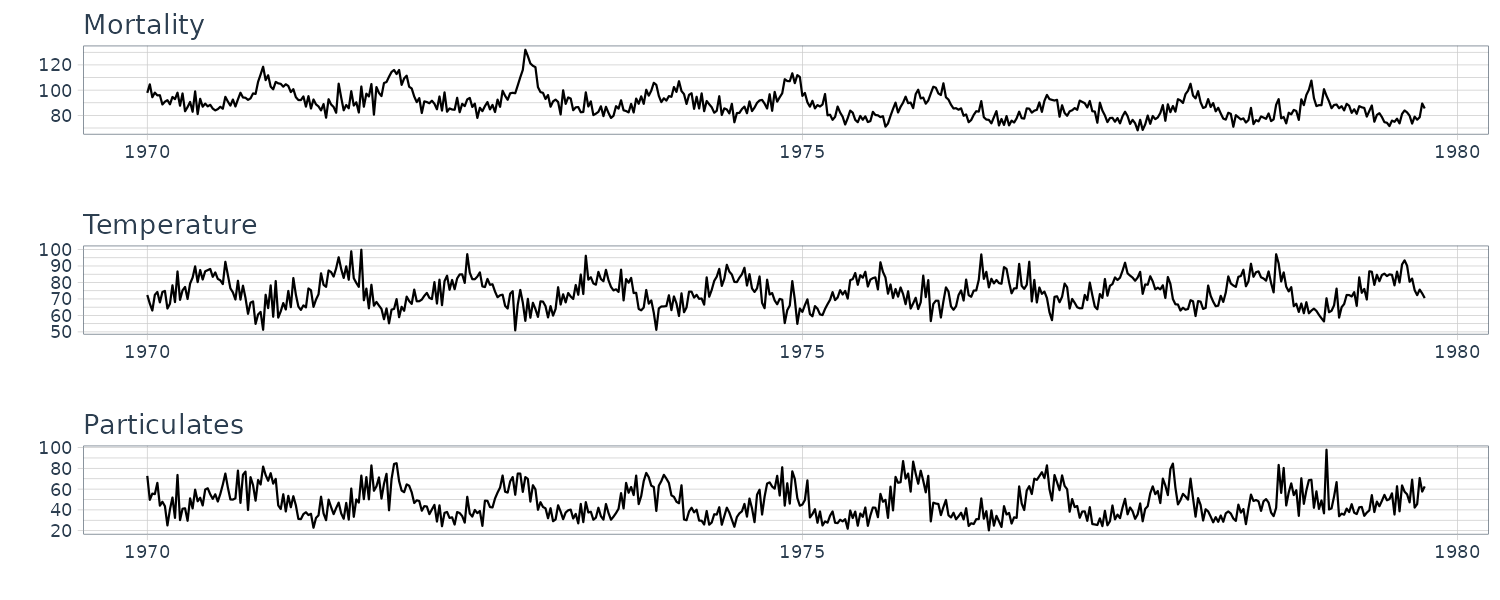
Example: Pollution, Temperature and Mortality
Let’s take a look at another example where we have more than one explanatory variables. We look at the possible effects of temperature and pollution on weekly mortality in LA county.
Taking a look at the time plots, we can see strong seasonal components in all 3 series:
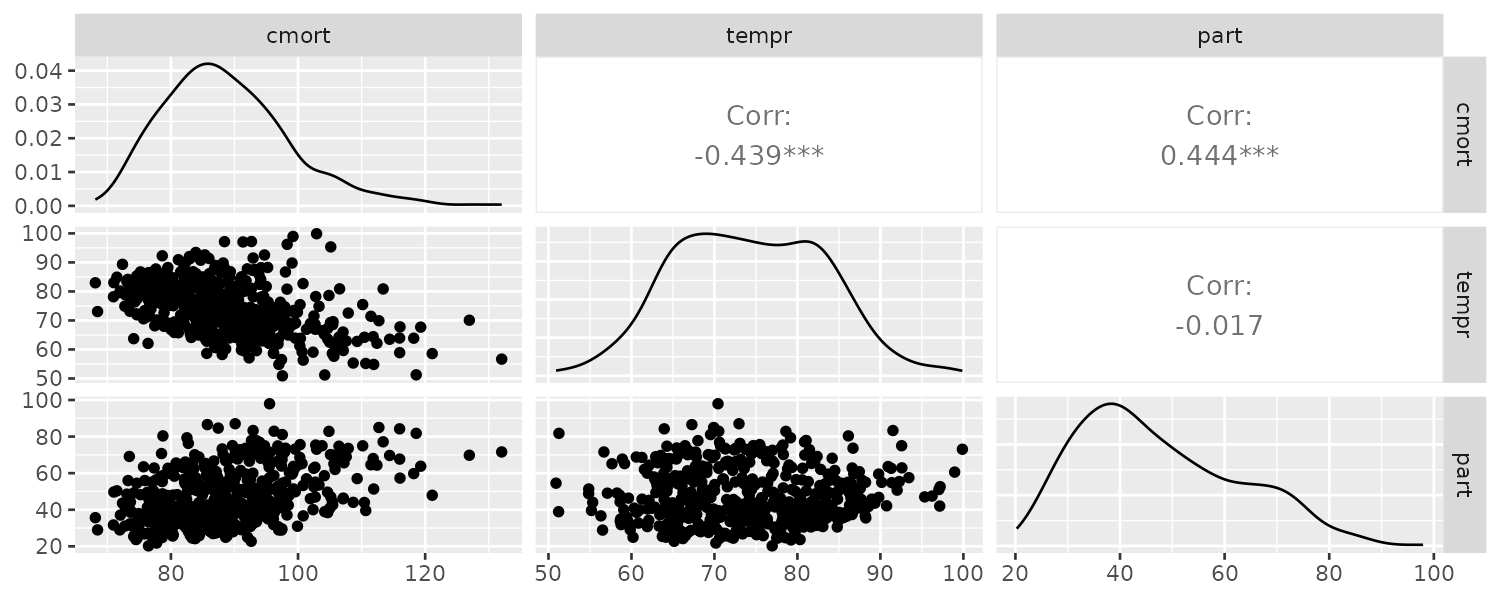
From the scatterplot, we can see strong linear relations between mortality and temperature and also pollutant. The mortality vs pollutants indicate a possible quadratic shape:
GGally::ggpairs(
dat,
columns = 2:4
)
We will attempt to fit the following models:
\[\begin{aligned} M_{t} &= \beta_{0} + \beta_{1}t + w_{t}\\ M_{t} &= \beta_{0} + \beta_{1}t + \beta_{2}(T_{t} - T_{\mu}) + w_{t}\\ M_{t} &= \beta_{0} + \beta_{1}t + \beta_{2}(T_{t} - T_{\mu}) + \beta_{3}(T_{3} - T_{\mu})^{2} + w_{t}\\ M_{t} &= \beta_{0} + \beta_{1}t + \beta_{2}(T_{t} - T_{\mu}) + \beta_{3}(T_{3} - T_{\mu})^{2} + \beta_{4}P_{4} + w_{t}\\ \end{aligned}\]Fitting the models in R:
fit1 <- lm(cmort ~ trend, data = dat)
fit2 <- lm(cmort ~ trend + temp, data = dat)
fit3 <- lm(cmort ~ trend + temp + temp2, data = dat)
fit4 <- lm(cmort ~ trend + temp + temp2 + part, data = dat)
> anova(fit1, fit2, fit3, fit4)
Analysis of Variance Table
Model 1: cmort ~ trend
Model 2: cmort ~ trend + temp
Model 3: cmort ~ trend + temp + temp2
Model 4: cmort ~ trend + temp + temp2 + part
Res.Df RSS Df Sum of Sq F Pr(>F)
1 506 40020
2 505 31413 1 8606.6 211.090 < 2.2e-16 ***
3 504 27985 1 3428.7 84.094 < 2.2e-16 ***
4 503 20508 1 7476.1 183.362 < 2.2e-16 ***We can see each subsequent model does better via the RSS/SSE.
Example: Regression With Lagged Variables
We saw the the Southern Oscillation Index (SOI) with a lag of 6 months is highly correlated with the Recruitment series. We therefore consider the following model:
\[\begin{aligned} R_{t} &= \beta_{0} + \beta_{1}S_{t-6} + w_{t} \end{aligned}\]Fitting the model in R:
dat <- tsibble(
t = rec$index,
soiL6 = lag(soi$value, 6),
rec = rec$value,
index = t
)
fit <- lm(rec ~ soiL6, data = dat)
> summary(fit)
Call:
lm(formula = rec ~ soiL6, data = dat)
Residuals:
Min 1Q Median 3Q Max
-65.187 -18.234 0.354 16.580 55.790
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 65.790 1.088 60.47 <2e-16 ***
soiL6 -44.283 2.781 -15.92 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 22.5 on 445 degrees of freedom
(6 observations deleted due to missingness)
Multiple R-squared: 0.3629, Adjusted R-squared: 0.3615
F-statistic: 253.5 on 1 and 445 DF, p-value: < 2.2e-16The fitted model is:
\[\begin{aligned} \hat{R}_{t} &= 65.79 - 44.28S_{t-6} \end{aligned}\]Exploratory Data Analysis
Trend Stationarity
The easiest form of nonstationarity to work with is trend stationary model:
\[\begin{aligned} x_{t} &= \mu_{t} + e_{t} \end{aligned}\]Where \(\mu_{t}\) is the trend and \(e_{t}\) is a stationary process. We will work with the detrended residual:
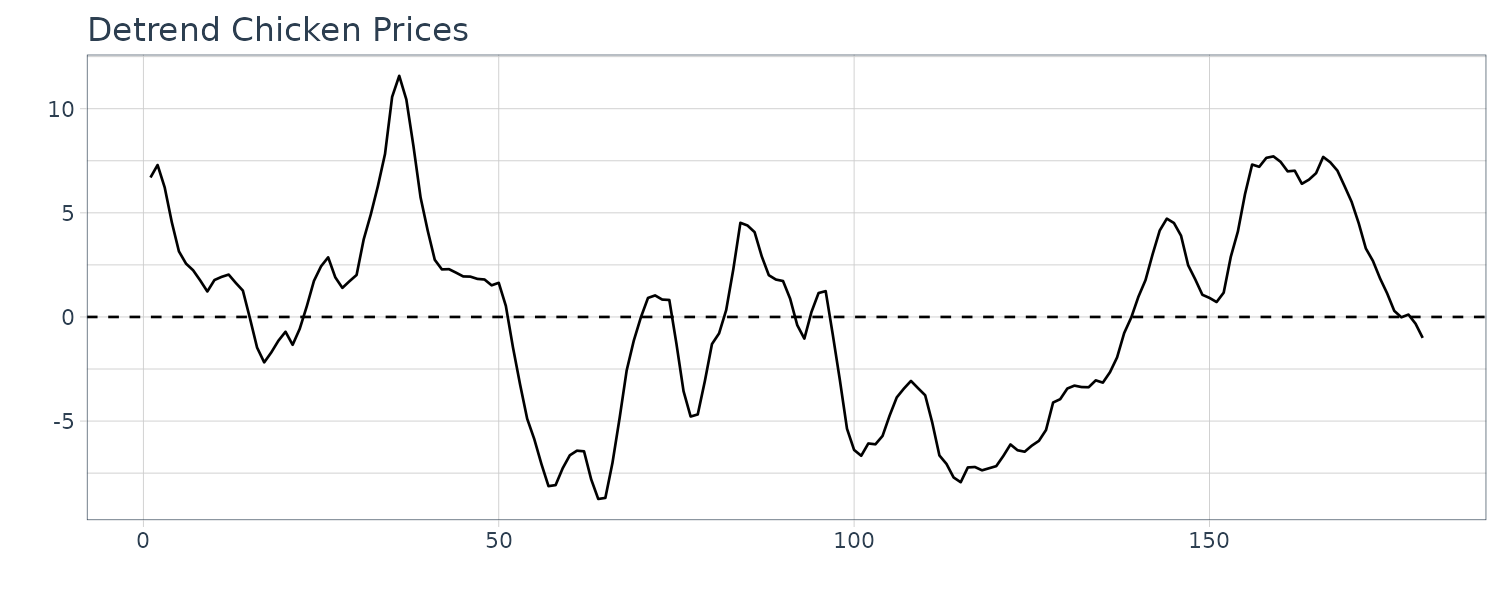
\[\begin{aligned} \hat{y}_{t} &= x_{t} - \hat{\mu}_{t} \end{aligned}\]Example: Detrending Chicken Prices
Recall the model for the chicken prices:
> summary(fit)
Call:
lm(formula = value ~ t, data = chicken)
Residuals:
Min 1Q Median 3Q Max
-8.7411 -3.4730 0.8251 2.7738 11.5804
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 58.583235 0.703020 83.33 <2e-16 ***
t 0.299342 0.006737 44.43 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.696 on 178 degrees of freedom
Multiple R-squared: 0.9173, Adjusted R-squared: 0.9168
F-statistic: 1974 on 1 and 178 DF, p-value: < 2.2e-16To obtain the detrended series:
\[\begin{aligned} \hat{y}_{t} &= x_{t} - 59 - 0.30 t \end{aligned}\]The plot:
The ACF plot:
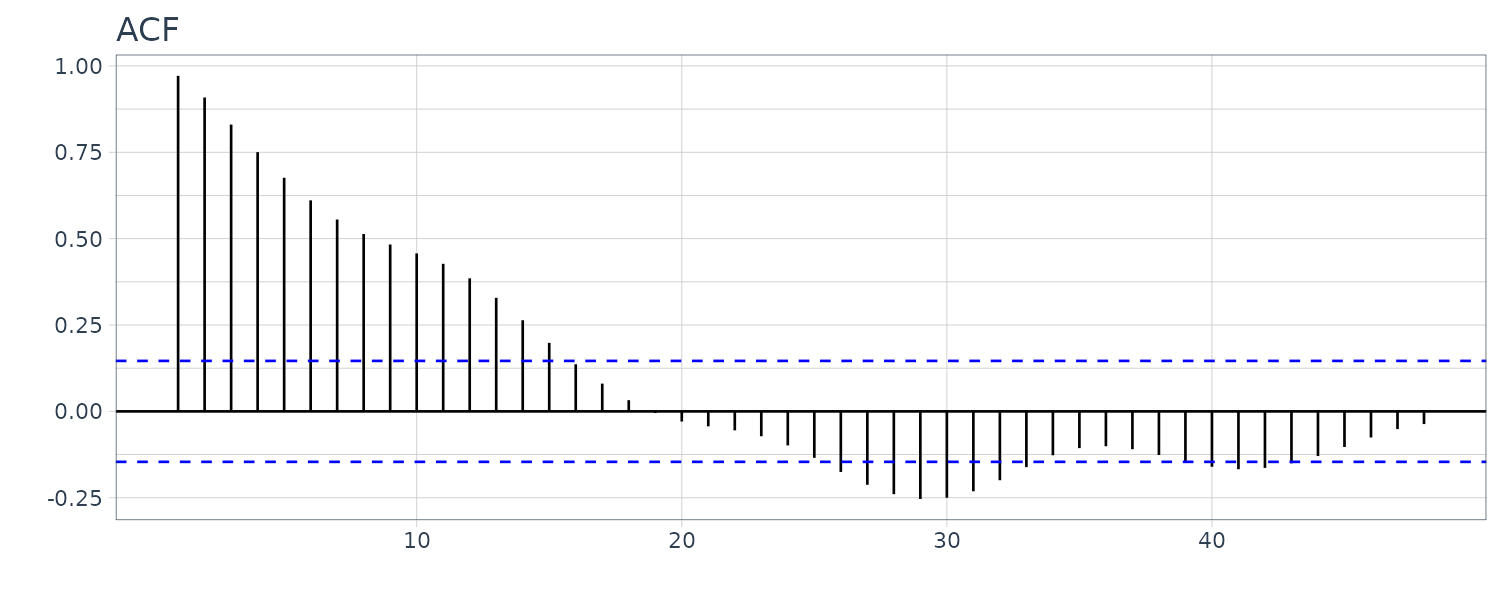
It is also possible to treat the model as a random walk with drift model:
\[\begin{aligned} \mu_{t} &= \delta + \mu_{t-1} + w_{t} \end{aligned}\]If the true source of the model is:
\[\begin{aligned} x_{t} &= \mu_{t} + e_{t} \end{aligned}\]Differencing the data will yield a stationary process:
\[\begin{aligned} x_{t} - x_{t-1} &= (\mu_{t} + e_{t}) - (\mu_{t-1} + e_{t-1})\\ &= (\mu_{t} - \mu_{t-1}) + (e_{t} - e_{t-1})\\ &= \delta + w_{t} + e_{t} - e_{t-1} \end{aligned}\]It is easy to show that \(e_{t}- e_{t-1}\) is stationary.
If an estimate of \(e_{t}\) is essential, then detrending may be more appropriate. If the goal is to coerce the data to stationarity, then differencing may be more appropriate. Differencing is also a viable tool if the trend is fixed. For example:
\[\begin{aligned} \mu_{t} &= \beta_{0} + \beta_{1}t\\ x_{t}- x_{t-1} &= (\mu_{t} + e_{t}) - (\mu_{t-1} + e_{t-1})\\ &= \beta_{0} + \beta_{1}t + e_{t} - (\beta_{0} + \beta_{1}(t-1) + e_{t-1})\\ &= \beta_{1}t - \beta_{1}t + \beta_{1} + e_{t} - e_{t-1}\\ &= \beta_{1} + e_{t} - e_{t-1} \end{aligned}\]One disadvantage of differencing is it does not yield an estimate for the stationary process \(e_{t}\).
Differencing (Backshift Operator)
As we have seen, the first difference eliminates a linear trend. A second difference can eliminate a quadratic trend, and so on.
We define the backshift operator as:
\[\begin{aligned} Bx_{t} &= x_{t-1}\\ B^{2}x_{t} &= B(Bx_{t})\\ &= B(x_{t-1})\\ &= x_{t-2}\\ B^{k} &= x_{t-k} \end{aligned}\]We also require that:
\[\begin{aligned} B^{-1}B &= 1 \end{aligned}\] \[\begin{aligned} x_{t} &= B^{-1}Bx_{t}\\ &= B^{-1}x_{t-1} \end{aligned}\]\(B^{-1}\) is known as the forward-shift operator.
We denote the first difference as:
\[\begin{aligned} \nabla x_{t} &= x_{t} - x_{t-1}\\ &= (1 - B)x_{t} \end{aligned}\]And second order difference:
\[\begin{aligned} \nabla^{2}x_{t} &= (1 - B)^{2}x_{t}\\ &= (1 - 2B + B^{2})x_{t}\\ &= x_{t} - 2x_{t-1} + x_{t-2}\\[5pt] \nabla(\nabla x_{t}) &= \nabla(x_{t} - x_{t-1})\\ &= (x_{t} - x_{t-1}) - (x_{t-1} - x_{t-2})\\ &= x_{t} - 2x_{t-1} + x_{t-2} \end{aligned}\]In general, differences of order d are defined as:
\[\begin{aligned} \nabla^{d} &= (1 - B)^{d} \end{aligned}\]Transformation
Sometimes transformations may be useful to equalize the variability of a time series. One example of such transformation is the log transform:
\[\begin{aligned} y_{t} &= \mathrm{log}(x_{t}) \end{aligned}\]Power transformations in the Box-Cox family are of the form:
\[\begin{aligned} y_{t} &= \begin{cases} \frac{x_{t}^{\lambda} - 1}{\lambda} & \lambda \neq 0\\ \mathrm{log}(x_{t}) & \lambda = 0 \end{cases} \end{aligned}\]Transformations are normally done to improve linearity and normality.
Lagged Scatterplot Matrix
The ACF gives a linear correlation of lags. However, the relationship might be nonlinear. The example in this section displays the lagged scatterplot of the SOI series. Lowess (locally weighted scatterplot smoothing) are plotted together with the scatterplot to help show the nonlinear relationship.
library(astsa)
lag1.plot(as.ts(soi), 12) 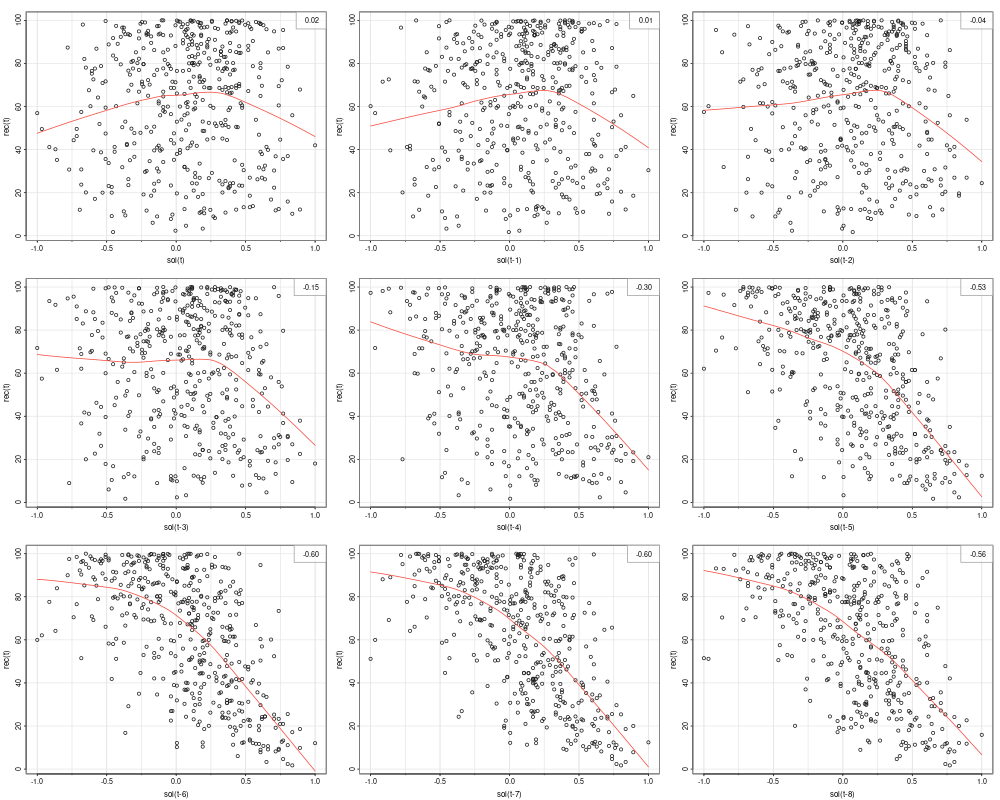
We can see the correlation is highest at t-6. However the relationship is nonlinear. In this case, we could add a dummy variable to implement a segmented regression (hockey stick):
\[\begin{aligned} R_{t} &= \beta_{0} + \beta_{1}S_{t-6} + \beta_{2}D_{t-6} + \beta_{3}D_{t-6} + w_{t}\\[5pt] R_{t} &= \begin{cases} \beta_{0} + \beta_{1}S_{t-6} + w_{t} & S_{t-6} < 0\\ (\beta_{0} + \beta_{2}) + (\beta_{1} + \beta_{3})S_{t-6} + w_{t} & S_{t-6} \geq 0 \end{cases} \end{aligned}\]dummy <- ifelse(soi$value < 0, 0, 1)
dat <- tibble(
rec = rec$value,
soi = soi$value,
soiL6 = lag(soi, 6),
dL6 = lag(dummy, 6)
) |>
mutate(
lowessx = c(
rep(NA, 6),
lowess(
soiL6[7:n()],
rec[7:n()]
)$x
),
lowessy = c(
rep(NA, 6),
lowess(
soiL6[7:n()],
rec[7:n()]
)$y
)
)
fit <- lm(rec ~ soiL6 * dL6, data = dat)
> summary(fit)
Call:
lm(formula = rec ~ soiL6 * dL6, data = dat)
Residuals:
Min 1Q Median 3Q Max
-63.291 -15.821 2.224 15.791 61.788
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 74.479 2.865 25.998 < 0.0000000000000002 ***
soiL6 -15.358 7.401 -2.075 0.0386 *
dL6 -1.139 3.711 -0.307 0.7590
soiL6:dL6 -51.244 9.523 -5.381 0.00000012 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 21.84 on 443 degrees of freedom
(6 observations deleted due to missingness)
Multiple R-squared: 0.4024, Adjusted R-squared: 0.3984
F-statistic: 99.43 on 3 and 443 DF, p-value: < 0.00000000000000022 Plotting the lowess and fitted curve:
dat$fitted <- c(rep(NA, 6), fitted(fit))
dat |>
ggplot(aes(x = soiL6, y = rec)) +
geom_point() +
geom_line(aes(y = lowessy, x = lowessx), col = "blue") +
geom_line(aes(y = fitted), col = "red") +
ggtitle("Rec vs SOIL6")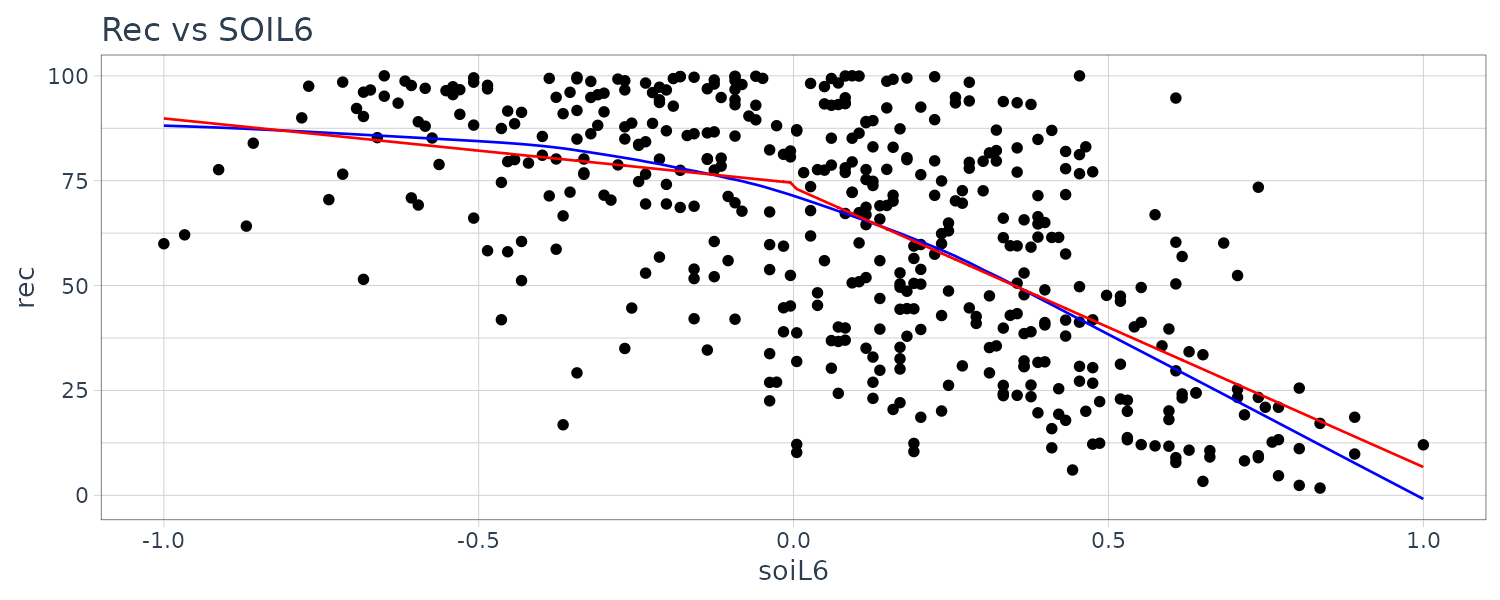
Smoothing
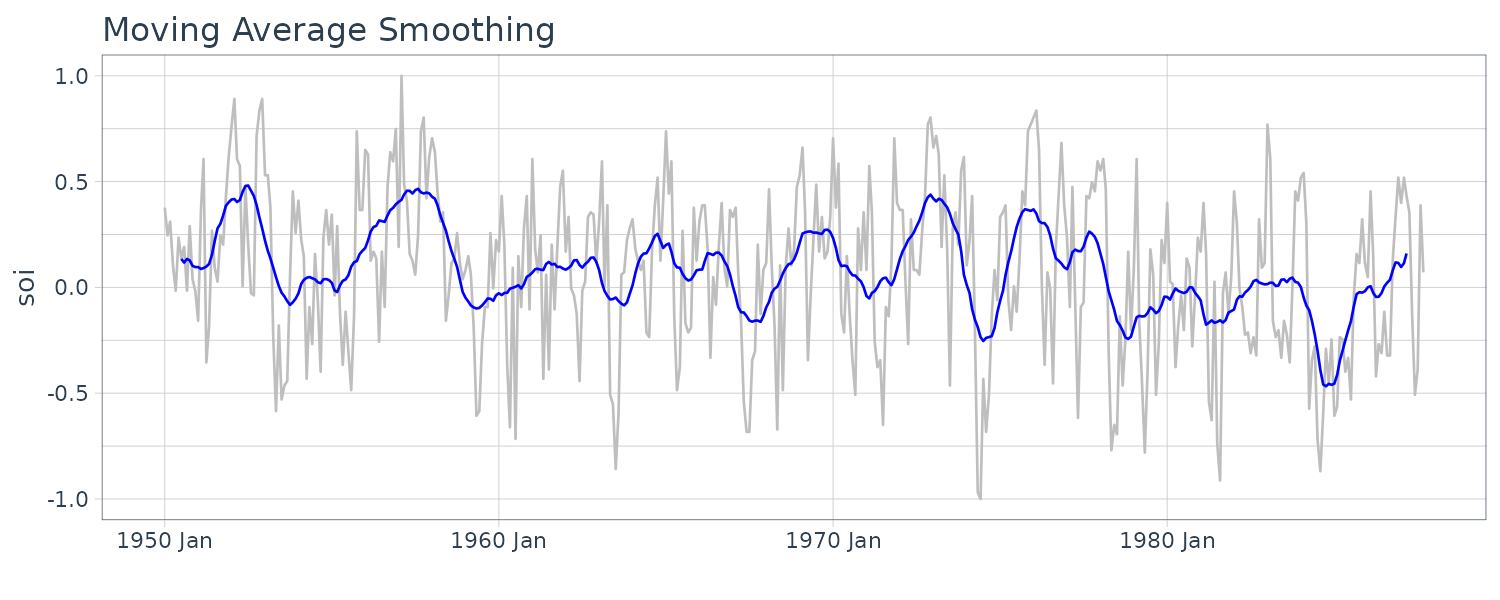
Moving Average Smoothing
If \(x_{t}\) represents the data observations, then:
\[\begin{aligned} m_{t} &= \sum_{j= -k}^{k}a_{j}x_{t-j}\\ a_j &= a_{-j} \geq 0 \end{aligned}\] \[\begin{aligned} \sum_{j=-k}^{k}a_{j} &= 1 \end{aligned}\]For example, using the monthly SOI series for \(k = 6\) using weights:
\[\begin{aligned} a_{0} &= a_{\pm 1} = \cdots = a_{\pm 5} = \frac{1}{12} \end{aligned}\] \[\begin{aligned} a_{\pm 6} &= \frac{1}{24} \end{aligned}\]weights <- c(.5, rep(1, 11), .5) / 12
dat <- tsibble(
t = soi$index,
soi = soi$value,
smth = stats::filter(
soi,
sides = 2,
filter = weights
),
index = t
)
Kernel Smoothing
Although the moving average smoothing highlight the EL Nino effect, the smoothing still look too choppy. We can obtain a smoother fit using normal distribution for the weights (kernel smoothing) rather than the boxcar-type weights above. “b” is the bandwidth and \(K()\) is known as the kernel function.
\[\begin{aligned} m_{t} &= \sum_{i=1}^{n}w_{i}(t)x_{i}\\ w_{i}(t) &= \frac{K\Big(\frac{t-i}{b}\Big)}{\sum_{j=1}^{n}K\Big(\frac{t-i}{b}\Big)} \end{aligned}\] \[\begin{aligned} K(z) &= \frac{1}{\sqrt{2\pi}}e^{\frac{-z^{2}}{2}} \end{aligned}\]To implement this in R, we use the “ksmooth” function. The wider the bandwidth, the smoother the result. In the SOI example, we use a value of \(b=12\) to corespond to approximately smoothing a little over a year.
dat$ksmooth <- ksmooth(
time(soi$index),
soi$value,
"normal",
bandwidth = 12
)$y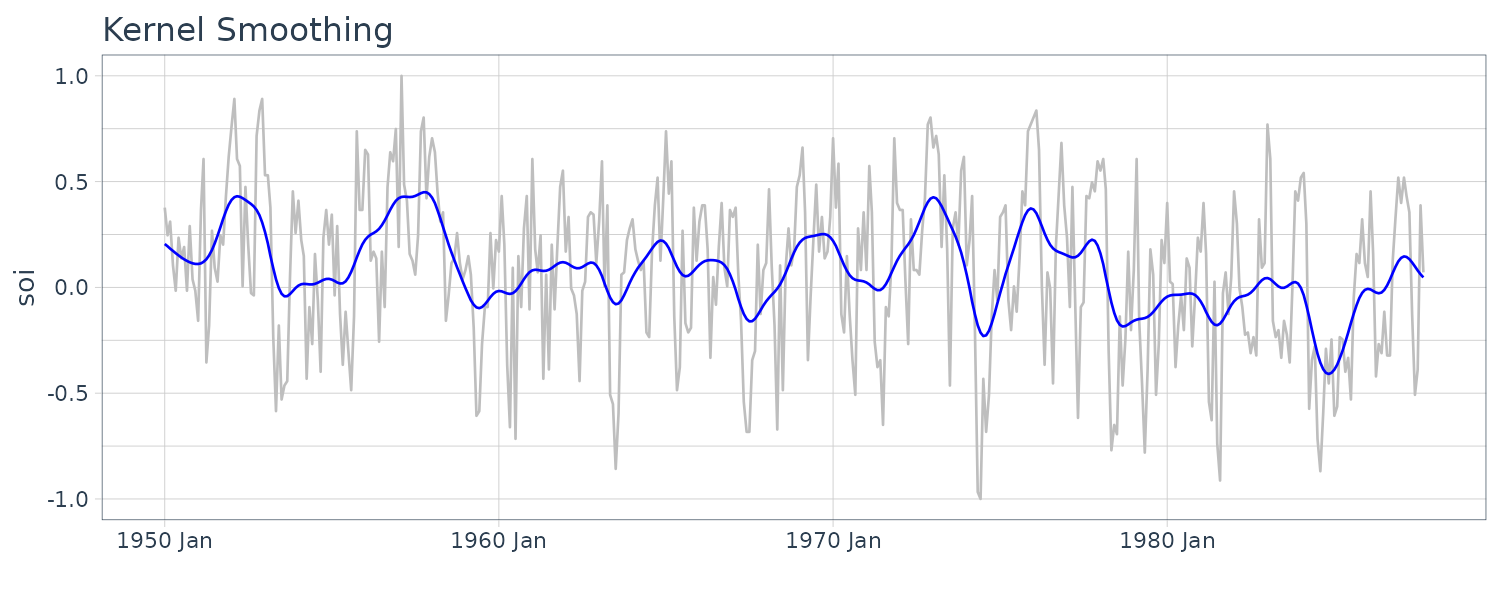
Lowess
Lowest is a method of smoothing that employs nearest neighbor local regression. The larger the fraction of nearest neighbors are included, the smoother the fit will be. We fit 2 lowess curve where one is smoother than the other:
dat$lowess1 <- lowess(soi$value, f = 0.05)$y
dat$lowess2 <- lowess(soi$value)$y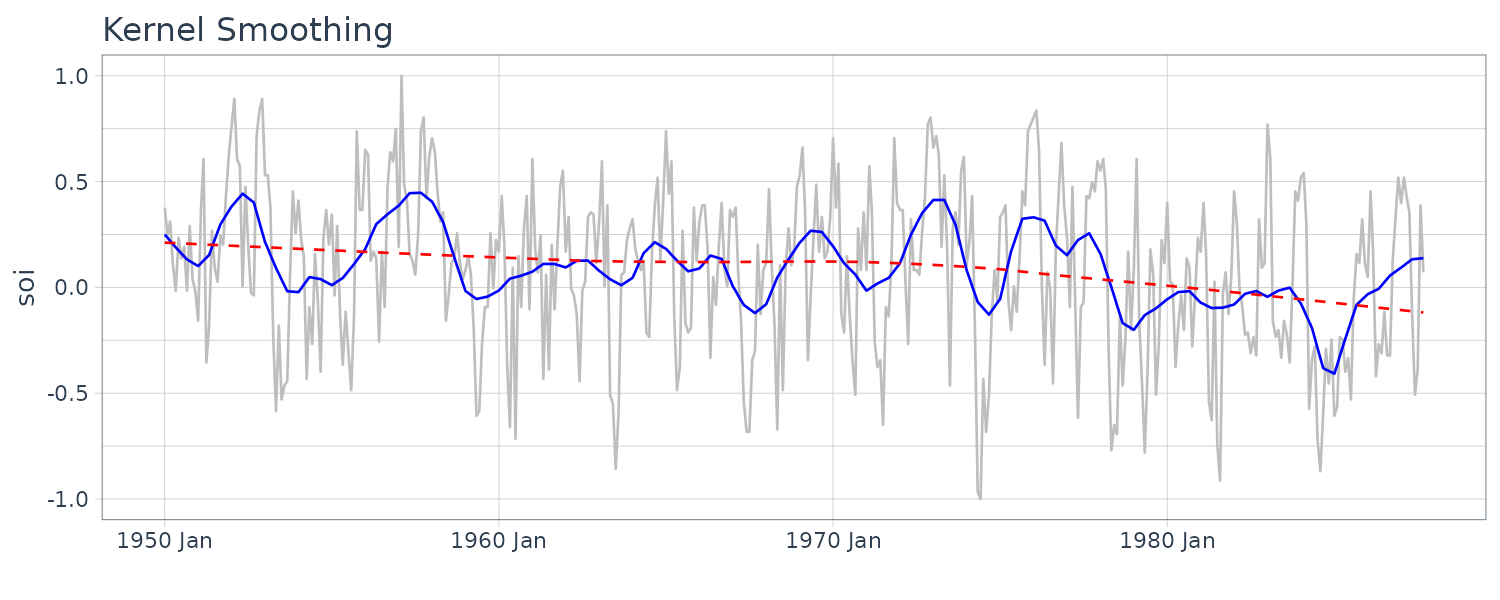
Smoothing Splines
Given a cubic polynomial:
\[\begin{aligned} m_{t} &= \beta_{0} + \beta_{1}t + \beta_{2}t^{2} + \beta_{3}t^{3} \end{aligned}\]Cubic splines divide the time into \(k\) intervals. The values \(t_{0}, t_{1}, \cdots, t_{k}\) are called knots. In each interval, a cublic polynomial is fit with conditions that the ends are connected.
For smoothing splines, the following objective function is minimized given a regularizing \(\lambda > 0\):
\[\begin{aligned} \sum_{t=1}^{n}(x_{t} - m_{t})^{2} + \lambda \int (m_{t}^{\prime\prime})^{2}\ dt \end{aligned}\]dat$spar1 <- smooth.spline(
time(soi$index),
soi$value,
spar = 0.5)$y
dat$spar2 <- smooth.spline(
time(soi$index),
soi$value,
spar = 1)$y
dat |>
autoplot(soi, color = "gray") +
geom_line(
aes(y = spar1),
color = "blue"
) +
geom_line(
aes(y = spar2),
color = "red",
linetype = "dashed"
) +
xlab("") +
ggtitle("Smoothing Spline") +
theme_tq()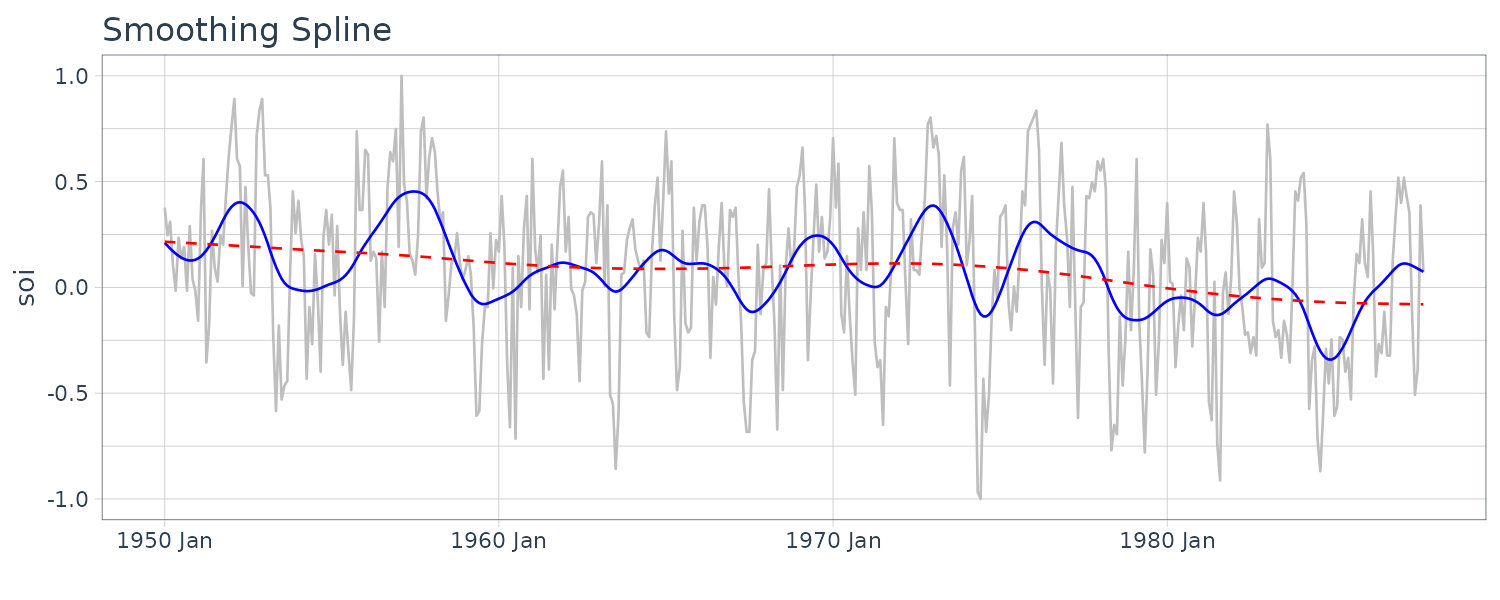
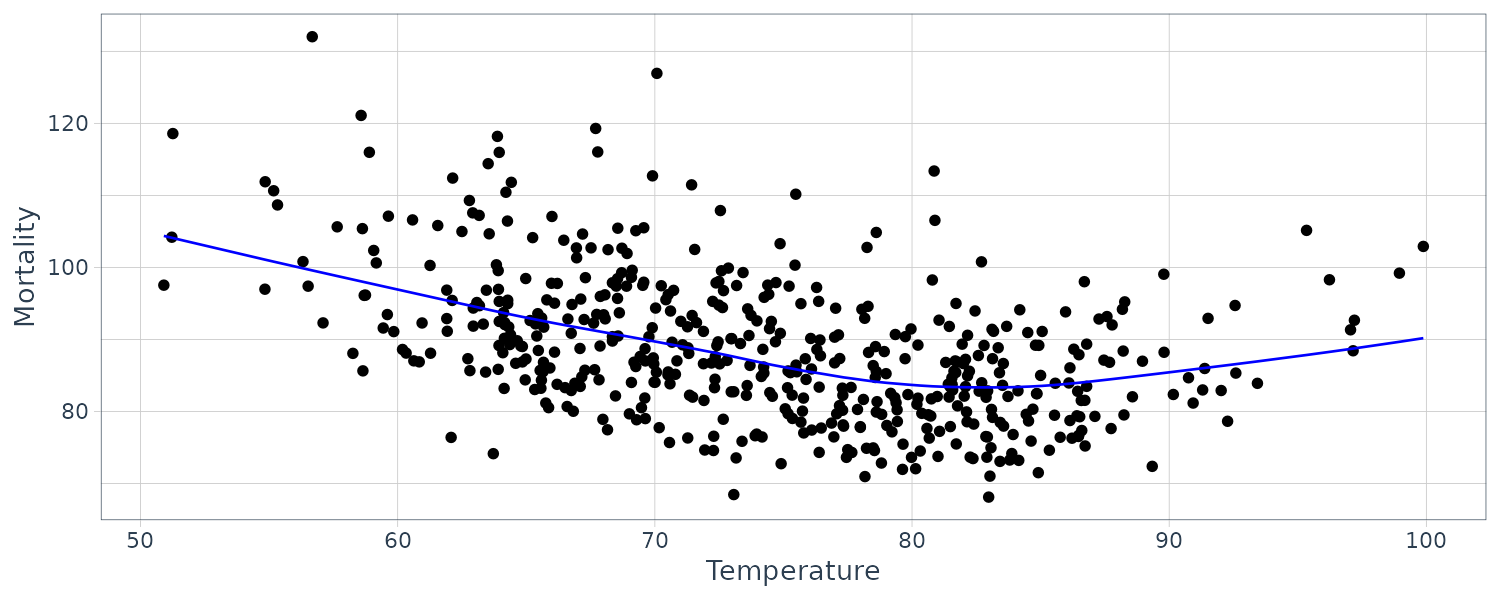
2D Smoothing
It is also possible to smooth one series over another. Using the Temperature and Mortality series data:
dat <- tibble(
tempr = tempr$value,
cmort = cmort$value,
lowess_y = lowess(tempr, cmort)$y,
lowess_x = lowess(tempr, cmort)$x
)
dat |>
ggplot(aes(x = tempr, y = cmort)) +
geom_point() +
geom_line(
aes(x = lowess_x, y = lowess_y),
color = "blue"
) +
xlab("Temperature") +
ylab("Mortality") +
theme_tq()